



Next: Concluding remarks
Up: Effect of core refractive
Previous: Derivation of perturbational expression
Contents
Now we assess the validity of the perturbation
expression (2.31). For the moderately lossy bent
waveguide configuration considered in Figure 2.14, the
estimation of the change in the phase propagation constants by the
perturbation expression agrees very well with the directly computed values.
Figure:
Phase propagation constants estimated by the perturbational
expression, for a bent waveguide configuration with
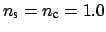 ,
,
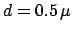 m,
m,
 m. Dashed lines denote
m. Dashed lines denote
 obtained by direct calculations, dots are reference points
obtained by direct calculations, dots are reference points
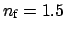 and
and
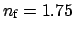 , and the slope of the solid
line segments is given by expression (2.31).
, and the slope of the solid
line segments is given by expression (2.31).
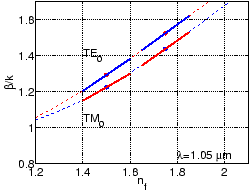 |
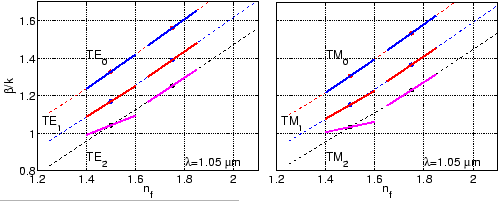
As an another example, for Figure 2.15, the
perturbational expression (2.31) is assessed for the
WGMs. For the moderately lossy fundamental and first order WGMs, the agreement is
excellent, but for the second order WGMs with considerable losses (e.g.
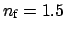 ,
,
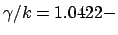 i
i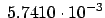 (TE
(TE ),
),
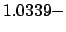 i
i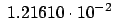 (TM
(TM )) there are major
deviations. Apparently, here the changes in the mode profiles and the
attenuation constants due to the core refractive index perturbation are not
negligible, such that the ansatz (2.26) is
not appropriate for these fields.
)) there are major
deviations. Apparently, here the changes in the mode profiles and the
attenuation constants due to the core refractive index perturbation are not
negligible, such that the ansatz (2.26) is
not appropriate for these fields.
Figure:
Phase propagation constants of WGMs evaluated by the
perturbational expression (2.31), for a bent
waveguide configuration with
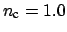 ,
,
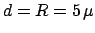 m. Interpretation of the curves is as for
Figure 2.14.
m. Interpretation of the curves is as for
Figure 2.14.
 |




Next: Concluding remarks
Up: Effect of core refractive
Previous: Derivation of perturbational expression
Contents
Kirankumar Hiremath
2005-09-23


![]() ,
,
![]() i
i![]() (TE
(TE![]() ),
),
![]() i
i![]() (TM
(TM![]() )) there are major
deviations. Apparently, here the changes in the mode profiles and the
attenuation constants due to the core refractive index perturbation are not
negligible, such that the ansatz (2.26) is
not appropriate for these fields.
)) there are major
deviations. Apparently, here the changes in the mode profiles and the
attenuation constants due to the core refractive index perturbation are not
negligible, such that the ansatz (2.26) is
not appropriate for these fields.
