



Next: Simulation results
Up: Effect of core refractive
Previous: Effect of core refractive
Contents
For a bent waveguide with the refractive index distribution
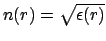 , let
, let
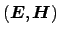 be the full electric and
magnetic field (2.1) for a given mode. Suppose that the
core refractive index is slightly perturbed, and the perturbed refractive
index distribution is given by
be the full electric and
magnetic field (2.1) for a given mode. Suppose that the
core refractive index is slightly perturbed, and the perturbed refractive
index distribution is given by
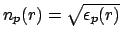 . For this
perturbation, assuming that the mode profile remains unchanged, the
corresponding perturbed mode
. For this
perturbation, assuming that the mode profile remains unchanged, the
corresponding perturbed mode
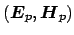 is approximated as
is approximated as
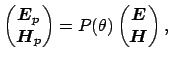 |
(2.26) |
where 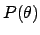 is an unknown function of the angular coordinate
is an unknown function of the angular coordinate
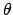 .
.
By using Lorentz's reciprocity theorem [43] in polar coordinates
to
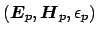 and
and
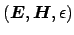 , one obtains
, one obtains
which upon inserting the ansatz given by Eq. (2.26) and after
simplifying reduces to
where
 is the unit vector in the angular direction.
is the unit vector in the angular direction.
Inserting the bent waveguide field ansatz given by
Eq. (2.1) and solving for 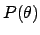 leads to
leads to
where  is a constant, the superscript
is a constant, the superscript 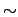 represents the mode
profile associated with the field. Thus the perturbed modal field is
represents the mode
profile associated with the field. Thus the perturbed modal field is
and the change in propagation constant
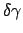 due to the perturbation
is given by
due to the perturbation
is given by
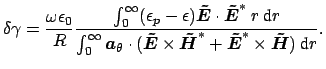 |
(2.29) |
Note that above expression can also be written in terms of modal fields
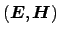 instead of mode profiles
instead of mode profiles
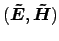 . The right hand side of Eq. (2.29) is a pure real
number. Therefore this expression, in fact, gives the change in the real part
of the propagation constant only. In Ref. [43] a similar expression
for the change in propagation constant for bulk uniform permittivity
perturbations of straight waveguides is derived by means of a variational
principle.
. The right hand side of Eq. (2.29) is a pure real
number. Therefore this expression, in fact, gives the change in the real part
of the propagation constant only. In Ref. [43] a similar expression
for the change in propagation constant for bulk uniform permittivity
perturbations of straight waveguides is derived by means of a variational
principle.
The use of asymptotic expansion of
H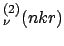 , given by
Eq. (2.5), reveals that, in the present case of bent waveguides,
the integral
, given by
Eq. (2.5), reveals that, in the present case of bent waveguides,
the integral
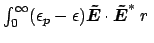 d
d is undefined for the upper limit
is undefined for the upper limit  , if
, if
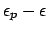 does not vanish for large radial coordinates. Still
for a uniform perturbation
does not vanish for large radial coordinates. Still
for a uniform perturbation
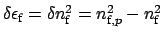 of the core
refractive index, it is well defined; in that case Eq. (2.29)
simplifies to
of the core
refractive index, it is well defined; in that case Eq. (2.29)
simplifies to
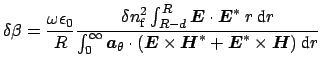 |
(2.30) |
where  and
and 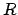 define the core interface as shown in Figure 2.1,
define the core interface as shown in Figure 2.1,
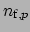 and
and
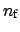 are perturbed and unperturbed core
refractive index respectively. For a small uniform perturbation of the core
refractive index, using Eq. (2.30), one can approximately write
are perturbed and unperturbed core
refractive index respectively. For a small uniform perturbation of the core
refractive index, using Eq. (2.30), one can approximately write
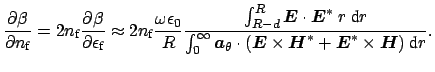 |
(2.31) |
Note that the integrals that occur in the above expression are well behaved.




Next: Simulation results
Up: Effect of core refractive
Previous: Effect of core refractive
Contents
Kirankumar Hiremath
2005-09-23
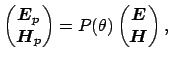
![]() and
and
![]() , one obtains
, one obtains
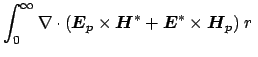 d
d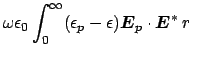 d
d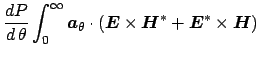 d
d d
d![]() leads to
leads to
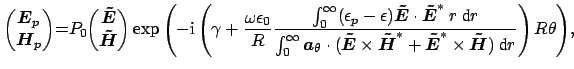
![]() , given by
Eq. (2.5), reveals that, in the present case of bent waveguides,
the integral
, given by
Eq. (2.5), reveals that, in the present case of bent waveguides,
the integral
![]() d
d![]() is undefined for the upper limit
is undefined for the upper limit ![]() , if
, if
![]() does not vanish for large radial coordinates. Still
for a uniform perturbation
does not vanish for large radial coordinates. Still
for a uniform perturbation
![]() of the core
refractive index, it is well defined; in that case Eq. (2.29)
simplifies to
of the core
refractive index, it is well defined; in that case Eq. (2.29)
simplifies to