Resonances

 In principle, all quantities that enter expressions (1.3), (1.4), (1.5) are wavelength dependent. Hence the proper way to compute the resonator spectrum would be to evaluate all relevant quantities in these expressions for a series of wavelengths.

A little more insight can be obtained if one accepts the approximation that if only a narrow wavelength interval needs to be considered, then the significant changes in the drop power and through power originate ``exclusively'' from the cosine terms in Equations (1.4), (1.5) that include the phase information.

To take into account the nonnegligible length $l$ of the cavity segments in the coupler regions, write the phase term as $\beta L - 2\varphi = \beta L_{\mbox{\scriptsize cav}} - \phi$, where $L_{\mbox{\scriptsize cav}}= 2 \pi R$ is the complete cavity length, and $\phi = 2 \beta l + 2 \varphi$ (a corresponding procedure is also applied to the phase term in the numerator of Equation (1.5)). Further consider only the wavelength dependence of the propagation constant $\beta$ as it appears explicitly in the term $\beta L_{\mbox{\scriptsize cav}} - \phi$. In this way, one incorporates the wavelength dependence of the phase change $\beta L_{\mbox{\scriptsize cav}}$ for the entire cavity, but disregards the wavelength dependence of the phase change $\phi$ that is introduced by the interaction with the port waveguides.

With the above approximation, resonances (i.e. maxima of the dropped power) are now characterized by singularities in the denominators of Equations (1.4), (1.5), which occur if $\cos{(\beta L_{\mbox{\scriptsize cav}} - \phi)} = 1$. This leads to the condition

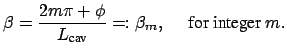$$\beta = \frac{2 m \pi + \phi}{L_{\mbox{\scriptsize cav}}} =: \beta_{m}, \hspace{0.5cm} \mbox{for integer } m.$$ (1.6)

For a resonant configuration, the dropped power is given by

$$P_{\mbox{\scriptsize D}}\vert _{\beta = \beta_m} = P_{\mbox{\scri... ...f {S}}_{\mbox{\scriptsize bb}}\vert^2 \mbox{e}^{\displaystyle - \alpha L} )^2}.$$ (1.7)

Note that properly computed values of ${\sf {S}}_{\mbox{\scriptsize sb}}$, ${\sf {S}}_{\mbox{\scriptsize bs}}$ and ${\sf {S}}_{\mbox{\scriptsize bb}}$ already include the losses along the parts of the cavity inside the couplers. Therefore $L$ in the Equation (1.7) (and in those places of Equations (1.4), (1.5) where attenuation is concerned) must not be replaced by $L_{\mbox{\scriptsize cav}}$.

In Chapter 4, we verify the validity of the above outlined approximation. As we shall see in the subsequent paragraphs, it provides quite useful insight into the spectral response of microresonators.