Ring-resonator theory

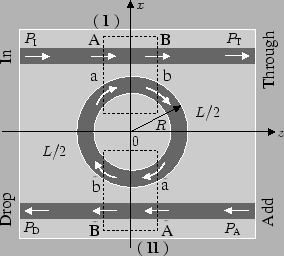
For the sake of further understanding, consider the typical abstract setting of a horizontally coupled circular microresonator as sketched in Figure 1.4. Two straight waveguides are evanescently coupled to the cavity. For ``well confined'' modes of the straight waveguide and cavity, one can expect that the interaction between the cavity modes and the port waveguide modes is localized around the region of the closest approach. Hence the device is functionally decomposed into two bent-straight waveguide couplers (I and II), which are connected to each other by the cavity segments, i.e. by pieces of bent waveguides. External connections are provided by the straight waveguides.

Figure 1.4: Functional decomposition of a microresonator into bent-straight waveguide couplers (shown by the dashed rectangles I and II), with the straight waveguide and the bent waveguide connections.

In this setting, as explained in the following paragraphs, the prediction of the spectral response of the resonator requires a description of the light propagation along the cavity segments, the analysis of the response of the bent-straight waveguide couplers, and finally a framework to combine these individual modules to predict the drop- and through-power. The subsequent discussion in this section is meant for structures involving monomodal straight waveguides and ring cavity. In Chapter 4, we extend it to the multimodal setting.