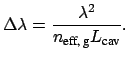Next: Full width at half
Up: Resonance characteristics
Previous: Resonance characteristics
Contents
The free spectral range (FSR) is defined as the wavelength difference
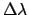 between two successive maxima of the dropped power (or minima of the
through power).
between two successive maxima of the dropped power (or minima of the
through power).
The resonant configuration next to a resonance found for
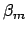 is approximated as
is approximated as
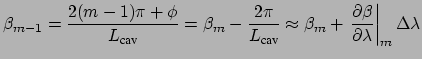 |
(1.8) |
where the right hand side is obtained as a first order Taylor series expansion
for the propagation constant around the 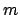 'th resonance wavelength;
'th resonance wavelength;
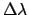 is the difference between the vacuum wavelengths corresponding to the
two resonant configurations.
is the difference between the vacuum wavelengths corresponding to the
two resonant configurations.
By virtue of homogeneity arguments [36] for the propagation constants
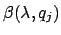 , viewed as a function of the wavelength
, viewed as a function of the wavelength 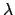 and
all geometrical parameters
and
all geometrical parameters 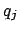 that define the cavity waveguide cross
section, one finds
that define the cavity waveguide cross
section, one finds
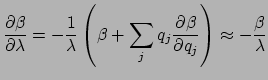 |
(1.9) |
for the wavelength dependence of the propagation constants in the cavity
loop. The same (crude) approximation can be obtained if one writes the
propagation constant in terms of vacuum wavenumber and effective mode index
as
 and neglects the wavelength
dependence of the effective index:
and neglects the wavelength
dependence of the effective index:
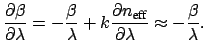 |
(1.10) |
This leads to the expression
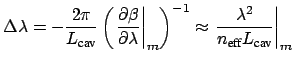 |
(1.11) |
for the free spectral range (FSR)
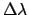 of the resonator around the
resonance of order
of the resonator around the
resonance of order 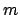 that is associated with the wavelength
that is associated with the wavelength 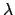 and
the effective mode index
and
the effective mode index
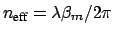 of the
cavity waveguide.
of the
cavity waveguide.
A more accurate and still simple expression can be obtained if one does not
introduce the approximations (1.9),
(1.10), i.e. if the wavelength dependence of 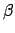 or
or
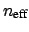 is explicitly incorporated. Customarily one can write
is explicitly incorporated. Customarily one can write
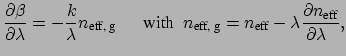 |
(1.12) |
where
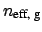 is the group effective index of the cavity
mode [35]. Then the free spectral range is given by
is the group effective index of the cavity
mode [35]. Then the free spectral range is given by
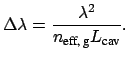 |
(1.13) |




Next: Full width at half
Up: Resonance characteristics
Previous: Resonance characteristics
Contents
Kirankumar Hiremath
2005-09-23
![]() is approximated as
is approximated as
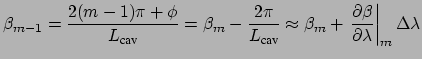
![]() , viewed as a function of the wavelength
, viewed as a function of the wavelength ![]() and
all geometrical parameters
and
all geometrical parameters ![]() that define the cavity waveguide cross
section, one finds
that define the cavity waveguide cross
section, one finds
![]() or
or
![]() is explicitly incorporated. Customarily one can write
is explicitly incorporated. Customarily one can write