



Next: Finesse and quality factor
Up: Resonance characteristics
Previous: Free spectral range
Contents
The full width at half maximum (FWHM) is a measure of the sharpness of the
resonance. As the name suggests, it is given as the width of the resonance
peak where the power drops to half of the resonance value.
A configuration that drops about half of the maximum power is realized for a
propagation constant
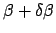 with
with
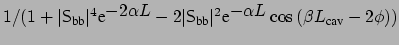
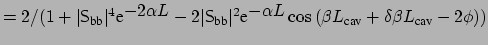 . Using the
second order approximation of the cosine terms around a resonant cavity
propagation constant, one obtains
. Using the
second order approximation of the cosine terms around a resonant cavity
propagation constant, one obtains
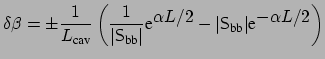 |
(1.14) |
for the shift in the propagation constants that distinguishes configurations
with the maximum and half of the maximum dropped power.
Using an approximation
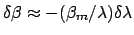 , analogous to
Equations (1.9),(1.10),
Equation (1.14) leads to an expression
, analogous to
Equations (1.9),(1.10),
Equation (1.14) leads to an expression
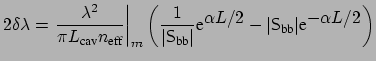 |
(1.15) |
which gives the full width at half maximum
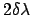 of the resonance
of order
of the resonance
of order 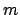 .
.




Next: Finesse and quality factor
Up: Resonance characteristics
Previous: Free spectral range
Contents
Kirankumar Hiremath
2005-09-23
![]() with
with
![]()
![]() . Using the
second order approximation of the cosine terms around a resonant cavity
propagation constant, one obtains
. Using the
second order approximation of the cosine terms around a resonant cavity
propagation constant, one obtains
![]() , analogous to
Equations (1.9),(1.10),
Equation (1.14) leads to an expression
, analogous to
Equations (1.9),(1.10),
Equation (1.14) leads to an expression