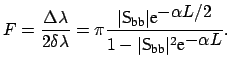 |
(1.16) |
The ability of the cavity to confine the field is described by the quality
factor ![]() . It is a measure of the sharpness of the transmission peak and
defined as the ratio of the resonance wavelength to the full width at half
maximum 1.2:
. It is a measure of the sharpness of the transmission peak and
defined as the ratio of the resonance wavelength to the full width at half
maximum 1.2:
For a circular resonator with radius ![]() and cavity length
and cavity length
![]() , one obtains
, one obtains
| (1.18) |
As before, the approximations according to
Equations (1.9), (1.10) can be
avoided by substituting the effective cavity mode index
![]() in
Equations (1.15), (1.17) by the effective group mode
index
in
Equations (1.15), (1.17) by the effective group mode
index
![]() as defined in
Equation (1.12).
as defined in
Equation (1.12).