Compact high contrast cavities

Now we compare CMT simulations with FDTD results for microring resonators with high index contrast and extremely small radius as presented in Ref. [56]. A ring cavity of radius $R=2.5 \,\mu$m is coupled to straight waveguides. The cavity and the straight waveguides have a core of width $w_{\mbox{\scriptsize c}}=w_{\mbox{\scriptsize s}}=0.3 \,\mu\mbox{m}$, and refractive index $n_{\mbox{\scriptsize c}}=n_{\mbox{\scriptsize s}}=3.2$, the background refractive index is $n_{\mbox{\scriptsize b}}=1$, and the separation distance is $g = \tilde{g} = 0.232 \,\mu$m. The fundamental mode of the In-port straight waveguide is launched with unit power. The response of this resonator is scanned over a wavelength range $[1.42, 1.62] \,\mu$m.

CMT calculations are carried out over a computational window $(x_{\mbox{\scriptsize l}}, z_{\mbox{\scriptsize i}})$ = $(0, -2)$ $\,\mu$m, $(x_{\mbox{\scriptsize r}}, z_{\mbox{\scriptsize o}})$= $(8, 2) \,\mu$m with stepsizes $h_{x} = 0.001 \,\mu$m, $h_{z} = 0.1 \,\mu$m. For the spectrum evaluation, quadratic interpolation is used with nodal wavelengths $\lambda = 1.42 \,\mu$m, $1.52 \,\mu$m, $1.62 \,\mu$m. At these nodal wavelengths, as shown in Table 4.1, the straight waveguides are bimodal and the bent waveguide (ring segment) is ``monomodal'' (i.e. the bend does not support other modal fields with reasonably low attenuation).

Table 4.1: Effective refractive indices of the modes of the straight waveguides and bent waveguide for the ringresonator of Section 4.4.3. Due to the high refractive index contrast, the bend modes have negligible losses.

	$\beta /k$ Straight waveguide		$\gamma /k$ Bent waveguide
$\lambda [\,\mu$m$]$	TE$_{0}$	TE$_{1}$	TE$_{0}$
$1.42$	$2.7959$	$1.4133$	$2.6332 -$   i$\ 0$
$1.52$	$2.7572$	$1.2578$	$2.5964 -$   i$\ 0$
$1.62$	$2.7186$	$1.1268$	$2.5598 -$   i$\ 0$

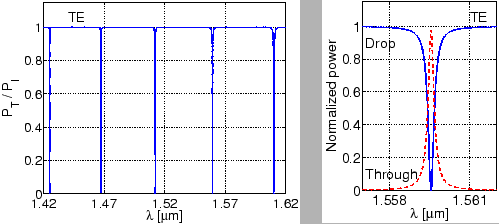
The resultant spectral response of the ringresonator is shown in Figure 4.11. Even though the straight waveguides are bimodal, due to the ``phase matching'' condition (see the values in Table 4.1), practically no power is coupled to the TE$_{1}$ straight waveguide mode. In good qualitative agreement with Ref. [56], the plots represent the output powers for the fundamental TE mode of the straight waveguide. The left plot of Figure 4.11 shows sharp resonances of the transmitted power, whereas the plot on the right side magnifies the resonance features at $\lambda_{\mbox{\scriptsize res}}=1.5596 \,\mu\mbox{m}$. At this resonance wavelength, the CMT simulations predict a full width at half maximum (FWHM) $2 \delta \lambda \approx 0.3$ nm, a quality factor $Q \approx 5200$, while Ref. [56] quotes $2 \delta \lambda \approx 0.3$ nm, $Q \approx 5000$.

Figure: Left: CMT Spectral response of the microring resonator of Section 4.4.3. Right: Resonance feature at $\lambda_{\mbox{\scriptsize res}}=1.5596 \,\mu\mbox{m}$. At this wavelength, almost $98\%$ of the input power is dropped.

A comparison of the resonance wavelengths obtained by the CMT simulations and the results of Ref. [56] is shown in Table 4.2. On the micron scale these results agree up to the second decimal place. For applications, where the positions of the resonance wavelengths on a large wavelength range (as e.g. in the left plot of Figure 4.11) is relevant, one can consider the difference relative to the free spectral range (FSR), i.e. look at the expression $\vert\lambda_{\mbox{\scriptsize res}}^{\mbox{\scriptsize CMT}} - \lambda_{\mbox{\scriptsize res}}^{\mbox{\scriptsize FDTD}}\vert/\mbox{FSR}$. For the TE$_{0}$ resonance at $\lambda_{\mbox{\scriptsize res}}^{\mbox{\scriptsize CMT}} = 1.5596 \,\mu\mbox{m}$, one obtains a small deviation of about $6\%$; in this respect, we find a reasonable agreement between FDTD and CMT simulations. On the other hand, for applications that involve a fine sampling of wavelengths, one might be interested in the deviation relative to the resonance width (FWHM), given by $\vert\lambda_{\mbox{\scriptsize res}}^{\mbox{\scriptsize CMT}} - \lambda_{\mbox{\scriptsize res}}^{\mbox{\scriptsize FDTD}}\vert/\mbox{FWHM}$. This leads to a deviation of about $930\%$, i.e. the computational values for the resonance positions become meaningless in this respect.

Note that for the present configuration, it is difficult to access the reliability of the CMT or the FDTD approach. The corresponding ring resonator with the high refractive index contrast represents an extreme configuration for the CMT approach. Also, the FDTD computations are seriously constrained by inherent numerical dispersion. Therefore we do not attempt a statement about which of the simulations corresponds to physical reality, what concerns the precise resonance positions.

Table 4.2: Comparison of resonance wavelengths for the ringresonator in Section 4.4.3 computed with FDTD (Ref. [56]) and CMT (present).

	$\lambda_{\mbox{\scriptsize res}} \ [\,\mu\mbox{m}]$
Ref. [56]	$1.4252$	$1.4675$	$1.5122$	$1.5624$	$1.6103$
Present	$1.4280$	$1.4715$	$1.5149$	$1.5596$	$1.613$1

By filling the interior of the ring waveguide in Section 4.4.3 with the core material, one obtains a microdisk resonator. For this structure, we now compare CMT results with Ref. [56]. As before, the TE$_{0}$ mode is excited at the In-port, the spectral response is computed with quadratic interpolation at nodal wavelengths $\lambda = 1.42 \,\mu$m$, 1.52 \,\mu$m$, 1.62 \,\mu$m. For the present setting, apart from the straight waveguide modes, the first three lower order cavity modes are sufficient as basis fields. Table 4.3 gives their effective refractive indices at the nodal wavelengths.

Table: Effective indices of the whispering gallery modes ( $w_{\mbox{\scriptsize c}}=R$) of the disk with radius $R=2.5 \,\mu$m, inner core refractive index $n_{\mbox{\scriptsize c}} = 3.2$, and external cladding refractive index $n_{\mbox{\scriptsize b}}=1.0$.

$\lambda [\,\mu$m$]$	$\gamma /k$ TE$_{0}$	$\gamma /k$ TE$_{1}$	$\gamma /k$ TE$_{2}$
$1.42$	$2.7482 -$   i$\ 0$	$2.3435 -$   i$\ 0$	$2.0153 -$   i$\ 6.4147 \cdot 10^{-11}$
$1.52$	$2.7298 -$   i$\ 0$	$2.3067 -$   i$\ 0$	$1.9638 -$   i$\ 1.0137 \cdot 10^{-9}$
$1.62$	$2.7119 -$   i$\ 0$	$2.2709 -$   i$\ 1.0878 \cdot 10^{-12}$	$1.9137 -$   i$\ 1.0653 \cdot 10^{-8}$

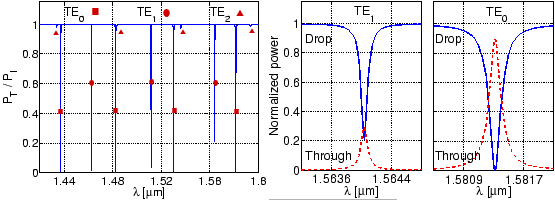
As in the case of the corresponding microring configuration, again here most of the input power is coupled to only the TE$_{0}$ mode of the straight waveguides. The spectral response of this microdisk resonator is shown in Figure 4.12; we again find a reasonable qualitative agreement with Ref. [56]. As evident from the plot on the left side, for the present configuration, only the TE$_{0}$ and TE$_{1}$ cavity modes play a significant role. Details of the resonances are shown in the associated plots.

Figure: CMT Spectral response of the microdisk resonator (left plot) of Section 4.4.3 with $w_{\mbox{\scriptsize c}}=R$. The central plot shows the resonance of the TE$_{1}$ cavity mode with $\lambda_{\mbox{\scriptsize res}} = 1.5640 \,\mu\mbox{m}$, $2 \delta \lambda \approx 0.1$ nm, and $Q = 14000$, whereas the right plot shows that of the TE$_{0}$ cavity mode with $\lambda_{\mbox{\scriptsize res}} =1.5813 \,\mu\mbox{m}$, $2 \delta \lambda \approx 0.2$ nm, and $Q = 7900$.

Note that these plots are obtained by quadratic interpolation of CMT results for scattering matrices $\sf {S}'$ and cavity segment propagation constants $\gamma_{\mbox{\scriptsize b}p}$ at just three nodal wavelengths, whereas to resolve such sharp features with FDTD simulations, one has to do FDTD calculations over extremely large time intervals, which turns out to be demanding in terms of computational effort.

The corresponding comparison of resonant wavelengths computed with CMT simulations and values of Ref. [56] is given in Table 4.4. As in the case of the previously discussed ringresonator, the remarks concerning the accuracy of the two simulation techniques with respect to the resonance positions apply to these results as well.

Table 4.4: Comparison of resonance wavelengths for the microdisk resonator as considered in Section 4.4.3.

	TE$_{0}$		TE$_{1}$		TE$_{2}$
	Ref. [56]	Present	Ref. [56]	Present	Ref. [56]	Present
	$1.4402$	$1.4373$	$1.4654$	$1.4626$	-	$1.4371$
$\lambda_{\mbox{\scriptsize res}}$	$1.4852$	$1.4823$	$1.5146$	$1.5115$	$1.4861$	$1.4833$
$[\,\mu$m]	$1.5332$	$1.5301$	$1.5672$	$1.5640$	$1.5390$	$1.5361$
	$1.5845$	$1.5813$	-	-	$1.5961$	$1.5935$