Microdisk resonator

We now consider the symmetrical microdisk resonator that is constituted by two of the multimode couplers discussed in Section 3.4.2. The computational setting and all parameters are identical to the data given in Section 3.4.2, for gap widths $g=\tilde{g}= 0.2\,\mu$m. The CMT description represents the optical field in the cavity as a superposition of the whispering gallery modes of Figure 3.8, where in principle

Figure 4.7: TE power spectrum of the microdisk resonator of Section 4.4.2. CMT analysis with different sets of basis modes; besides the mode of the straight waveguide, only one bend field (TE$_0$, TE$_1$, TE$_2$, left), or the two, three, or four lowest order whispering gallery modes (right) are taken into account.

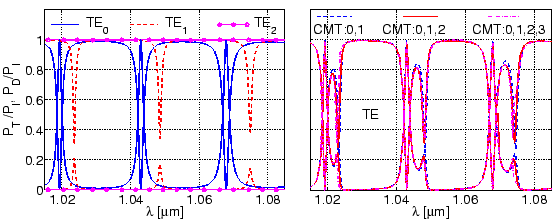
one must expect that more or less pronounced features related to all of these basis fields appear in the resonator spectrum. Figure 4.7 allows to investigate the significance of the individual cavity modes on the spectral response predicted by the CMT analysis.

The plots of Figure 4.7 show the spectral response as obtained by CMT computations where, besides the mode of the straight waveguide, different sets of bend modes are used as basis fields. The curves related to calculations with single cavity modes (left) exhibit only specific extrema of the full spectrum with similar extremal levels; obviously these resonances can be assigned to the respective (TE$_0$ or TE$_1$) whispering gallery mode. As these modes circulate along the cavity with their different propagation constants, individual resonance conditions are satisfied in general at different wavelengths. Apparently the regime discussed at the end of Section 4.1 is realized here (cf. also the tiny bend mode cross coupling coefficients $\vert{\sf {S}}_{\mbox{\scriptsize b}o,\mbox{\scriptsize b}i}\vert^2$ in Figure 3.11).

While the fundamental and first order bend mode are essential for the present resonator, inclusion of the second order whispering gallery mode into the CMT analysis leads only to minor, the third order bend field to no visible changes of the curves in the right plot of Figure 4.7. Thus for this microdisk configuration it is sufficient to take into account the three lowest order cavity modes as basis fields to predict reliably the spectral response.

The left plot of Figure 4.8 allows to validate the interpolation approach of Section 4.3 for the spectrum evaluation; just as in Section 4.4.1 one finds that the quadratic interpolation of the scattering matrix coefficients and propagation constants leads to curves that are almost indistinguishable from the directly computed results. The spectrum computed with the approximation technique of Section 1.4.3 is shown in the plots on right side Figure 4.8. Using constant scattering matrices ${\sf {S}}'$, ${\sf {\tilde{S}}}'$ evaluated at $\lambda=1.05\,\mu$m along with the wavelength dependent cavity mode propagation constants, computed spectrum (dashed line) agrees quite well with the strictly wavelength dependent calculations (solid line). On the scale of the figure, the locations of the resonances predicted by this approximation match with those corresponding to the ``direct'' calculations; but away from the reference wavelength $\lambda=1.05\,\mu$m, the TE$_{1}$ extrema levels differ slightly. Anyway, here one can accept the line of arguments in Section 1.4.3 as a very good approximation.

Figure: Left: CMT spectra (four basis modes) for the resonator setting as in Figure 4.7 computed directly, and by interpolation of data evaluated at the nodal wavelengths $1.015\,\mu$m, $1.085\,\mu$m (linear) or $1.015\,\mu$m, $1.05\,\mu$m, $1.085\,\mu$m (quadratic interpolation). Right: Spectrum computed with direct CMT calculations (solid line) and with the approximation technique in Section 1.4.3 (dashed line).

Figure 4.9 compares the CMT spectra for TE and TM polarized light with rigorous FDTD calculations, where the simulation parameters are identical to those given in Section 4.4.1. There is a quite satisfactory agreement; as before minor deviations occur for the configurations with highly radiative, strongly interacting, and less regular fields in the TM case. The computational effort required for the CMT analysis is about two orders of magnitude lower than the effort required for the FDTD simulations.

Figure 4.9: Power transmission through the microdisk resonator of Section 4.4.2, CMT and FDTD spectra (top) for TE (left) and TM polarized modes (right). The plots in the second row show the wavelength dependence of the amplitudes $\vert b_q\vert^2$ of the whispering gallery modes inside the cavity at port b (see Figure 4.1).

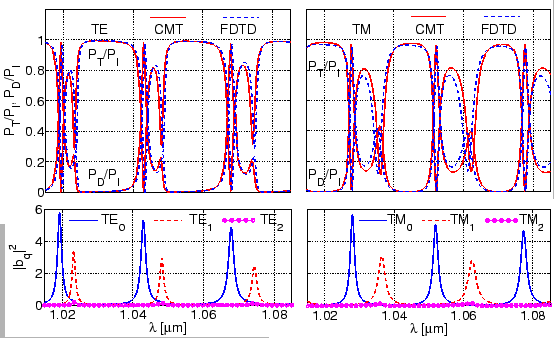As an alternative to the computations of Figure 4.7, the inspection of the amplitudes of the basis modes that establish inside the cavity for varying wavelength provides a direct means for labeling the spectral features. The plots in the second row of Figure 4.9 identify the narrower, most pronounced resonances as belonging to the fundamental cavity modes, while the wider, less pronounced peaks are due to the first order whispering gallery fields.

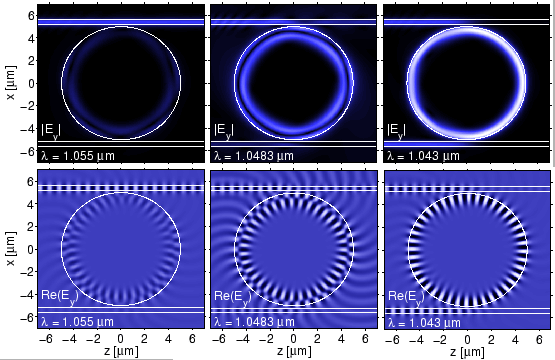
Figure 4.10 gives an impression of the field distributions that accompany the resonance phenomena. Off resonance, most of the input power is directly transferred to the Through-port. At the wavelength corresponding to the minor resonance, the field pattern in the cavity exhibits a nearly circular nodal line that corresponds to the radial minimum in the profile of the first order whispering gallery mode (cf. Figure 3.8). According to Figure 4.9, here the first order mode carries most of the power inside the cavity. The deviation form the circular pattern is caused by the interference with the fundamental bend mode, which is also excited at this wavelength with a small power fraction. The major resonance related to the fundamental mode is of higher quality, with much larger intensity in the cavity, almost full suppression of the waves in the Through-port and nearly complete drop of the input power.

Figure 4.10: Field examples for the microdisk resonator of Section 4.4.2, CMT simulations with four basis modes, absolute value $\vert E_y\vert$ of the principal component of the TE fields (top), and snapshots of the real physical electric field (bottom). The wavelengths correspond to an off-resonance configuration (left) and to minor (center) and major resonances (right). The color scale levels of the plots in each row are comparable.