



Next: Remarks on the numerical
Up: Bent waveguide model
Previous: Bend mode normalization
Contents
Orthogonality of bend modes
If the bend mode profiles are employed as basis elements for an expansion of a
general optical field in the bend structure, the orthogonality properties of
these modes become relevant: Projecting on the basis modes allows to relate
the modal amplitudes to the given arbitrary field. As a consequence of the
leaky nature of the complex bend modes, the orthogonality relations involve
nonconjugate versions of the field profiles.2.3
Let
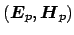 and
and
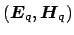 be the
electromagnetic fields (2.1) of bend modes with
propagation constants
be the
electromagnetic fields (2.1) of bend modes with
propagation constants
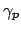 and
and
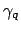 , respectively, that are
supported by the same bent waveguide. We start with the identity
, respectively, that are
supported by the same bent waveguide. We start with the identity
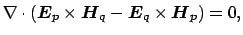 |
(2.13) |
which is a straightforward consequence of the Maxwell equations.
Consider the integral of Eq. (2.13) over an angular segment
![$ \Omega =
[0, \tilde{r}] \times [\theta, \theta + \Delta \theta]$](img358.png) in the waveguide
plane, specified by intervals of the polar coordinates:
in the waveguide
plane, specified by intervals of the polar coordinates:
After simplification of Eq. (2.14) by means of the Gauss theorem and
a Taylor series expansion around  , for small, nonzero
, for small, nonzero
 one obtains
one obtains
i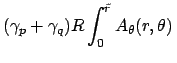 d d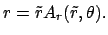 |
(2.15) |
In order to evaluate the limit
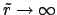 of the right
hand side,
of the right
hand side, 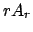 is expressed in terms of the basic mode profile components
is expressed in terms of the basic mode profile components
 and
and 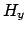 , with the help of Eqs. (2.2, 2.3):
, with the help of Eqs. (2.2, 2.3):
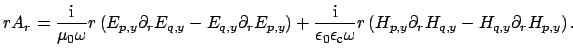 |
(2.16) |
Here
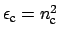 is the permittivity in the
exterior region of the bend (constant for large radii). In this region, the
basic components
is the permittivity in the
exterior region of the bend (constant for large radii). In this region, the
basic components
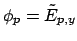 or
or
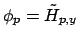 of
modal solutions (2.6) are given by Hankel functions of second
kind i.e.
of
modal solutions (2.6) are given by Hankel functions of second
kind i.e.
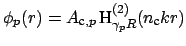 ,
which, for large radial coordinate, assume the asymptotic forms
,
which, for large radial coordinate, assume the asymptotic forms
By using these expressions, the limits
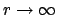 of the
individual parts of Eq. (2.16) can be shown to vanish
of the
individual parts of Eq. (2.16) can be shown to vanish
![$\displaystyle \lim_{r \rightarrow \infty} \left[ r(\phi_{p} \partial_r \phi_{q} - \phi_{q} \partial_r \phi_{p})\right] = 0.$](img374.png) |
(2.18) |
This leads to the identity
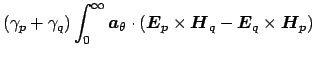 d d |
(2.19) |
where
 is the unit vector in the azimuthal (
is the unit vector in the azimuthal (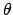 -)
direction.
-)
direction.
After inspecting Eqs. (2.2), (2.3), one readily sees that
the fields
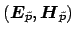 and the propagation
constant
and the propagation
constant
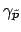 with
with
describe a valid modal solution of the bend problem. By writing out the
expression (2.19) for the quantities with indices 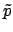 and
and 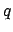 , by applying the transformation (2.20), and by observing
that
, by applying the transformation (2.20), and by observing
that
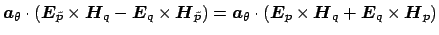 , Eq. (2.19) can be
given the form
, Eq. (2.19) can be
given the form
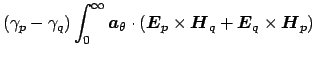 d d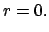 |
(2.21) |
Motivated by the result (2.21), we define the following
symmetric, complex valued product2.4 of two
(integrable) electromagnetic fields
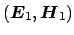 and
and
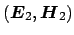 , given in the polar coordinate system of the bend structure:
, given in the polar coordinate system of the bend structure:
Obviously, the integrand vanishes if fields of different (2-D) polarizations
are inserted, i.e. TE and TM bend modes are orthogonal with respect to
(2.22). One easily checks that the product is also zero, if the
forward and backward versions (two fields with their components related by the
transformation (2.20)) of a bend mode are inserted. Finally,
according to Eq. (2.21), two nondegenerate bend modes with
propagation constants
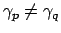 that are supported by the same
bend structure are orthogonal with respect to the product (2.22).
These formal statements hold for pairs of the fields (2.1)
with the full space and time dependence, for the expressions excluding the
time dependence, as well as for pairs of pure mode profiles that depend on the
radial coordinate only.
that are supported by the same
bend structure are orthogonal with respect to the product (2.22).
These formal statements hold for pairs of the fields (2.1)
with the full space and time dependence, for the expressions excluding the
time dependence, as well as for pairs of pure mode profiles that depend on the
radial coordinate only.
Assuming that for a given bend configuration a discrete, indexed set of
nondegenerate modal fields
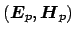 with (pairwise different)
propagation constants
with (pairwise different)
propagation constants 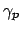 is considered, the orthogonality properties
can be stated in the more compact form
is considered, the orthogonality properties
can be stated in the more compact form
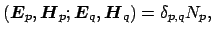 |
(2.23) |
with
and
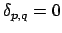 for
for 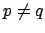 ,
,
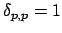 . For mode sets of
uniform polarization and uniform direction of propagation, it can be
convenient to write the orthogonality properties in terms of the basic mode
profile components
. For mode sets of
uniform polarization and uniform direction of propagation, it can be
convenient to write the orthogonality properties in terms of the basic mode
profile components
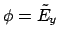 (TE) or
(TE) or
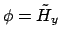 (TM).
This leads to the relations
(TM).
This leads to the relations
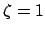 for TE, and
for TE, and
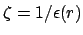 for TM polarization, which
differ from the corresponding familiar expressions for straight dielectric
slab waveguides by the appearance of the inverse radial coordinate
for TM polarization, which
differ from the corresponding familiar expressions for straight dielectric
slab waveguides by the appearance of the inverse radial coordinate  only.
According to Eq. (2.17),
only.
According to Eq. (2.17), 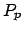 is obviously bounded. Note,
however, that here
is obviously bounded. Note,
however, that here 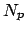 and
and 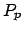 are complex valued quantities.
are complex valued quantities.
An alternative derivation of Eq. (2.24) starts with the eigenvalue
equation (2.4), written out for two different modal solutions.
Each equation is multiplied by the other mode profile, one subtracts the
results, and integrates over the radial axis. This leads to an equation with
the difference of the squared propagation constants times the integral of
Eq. (2.24) on one side, and with a limit as in
Eq. (2.16) on the other. Then the reasoning of
Eqs. (2.17, 2.18) can be applied to obtain the desired
result. All sets of bend mode profiles shown in the following sections satisfy
the relations (2.23) or (2.24), respectively, up to the
accuracy that can be expected from the computational procedures.




Next: Remarks on the numerical
Up: Bent waveguide model
Previous: Bend mode normalization
Contents
Kirankumar Hiremath
2005-09-23
![]() and
and
![]() be the
electromagnetic fields (2.1) of bend modes with
propagation constants
be the
electromagnetic fields (2.1) of bend modes with
propagation constants
![]() and
and
![]() , respectively, that are
supported by the same bent waveguide. We start with the identity
, respectively, that are
supported by the same bent waveguide. We start with the identity
![]() in the waveguide
plane, specified by intervals of the polar coordinates:
in the waveguide
plane, specified by intervals of the polar coordinates:
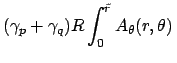 d
d![]() and the propagation
constant
and the propagation
constant
![]() with
with
![]() and
and
![]() , given in the polar coordinate system of the bend structure:
, given in the polar coordinate system of the bend structure:
![]() with (pairwise different)
propagation constants
with (pairwise different)
propagation constants ![]() is considered, the orthogonality properties
can be stated in the more compact form
is considered, the orthogonality properties
can be stated in the more compact form
 d
d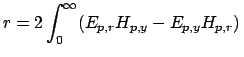 d
d![]() for
for ![]() ,
,
![]() . For mode sets of
uniform polarization and uniform direction of propagation, it can be
convenient to write the orthogonality properties in terms of the basic mode
profile components
. For mode sets of
uniform polarization and uniform direction of propagation, it can be
convenient to write the orthogonality properties in terms of the basic mode
profile components
![]() (TE) or
(TE) or
![]() (TM).
This leads to the relations
(TM).
This leads to the relations