- ...
``photonics''1.1
- Optronics -- opto-electronics -- is
about using modern optical technology along with conventional
microelectronics technology. Many times, the terms ``optics'' and
``photonics'' are used interchangeably, and the distinction between them is
rather vague. Optics is a quite wide field dealing with light in different
contexts, spanning from geometrical optics (dealing with lenses, prisms,
free space transmission, etc.) to quantum optics (dealing with
light-matter interaction).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
maximum 1.2
- In a time domain setting, the
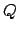 factor is defined as the
ratio of the optical power stored in the cavity to the cycle averaged power
radiated out of the cavity [37]. Therefore the larger the Q factor,
the longer the optical field is trapped inside the cavity.
factor is defined as the
ratio of the optical power stored in the cavity to the cycle averaged power
radiated out of the cavity [37]. Therefore the larger the Q factor,
the longer the optical field is trapped inside the cavity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... indices 1.3
- Other factors like
anisotropy, material attenuation, side wall roughness play a role in real
devices, but these are out of scope of the present work.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... already 1.4
- For the present work, we use 2-D straight
waveguide mode solver by Dr. Manfred Hammer. See
www.math.utwente.nl/ hammer/Metric/ for further details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... modes.2.1
- Partly these notions originate from
the use of a ray picture for the description of bent waveguides, or from
approximate models in terms of ``equivalent'' leaky straight waveguide
profiles. We will avoid these viewpoints in the present work.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
solved2.2
- In an alternative approach, where one looks at time domain
resonances of circular cavities, a similar procedure as outlined here
[44,39] leads to precisely the same equation (cf. the remarks in
the introduction). In that case, Eq. (2.7) is to be solved for
complex valued resonance frequencies
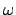 , for given integer azimuthal
mode numbers
, for given integer azimuthal
mode numbers 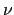 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... profiles.2.3
- An approximate
orthogonality relation involving complex conjugates of one of the mode
profiles is derived in Ref. [91], valid in the limit of large
bend radius (i.e. for almost straight waveguides).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... product2.4
- Cf. the standard variants of
orthogonality relations for straight dielectric waveguides made of
attenuating materials, as introduced e.g. in Ref. [43]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Uranus043.1
- For comprehensive information about finite
difference time domain methods, see www.fdtd.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.