



Next: Orthogonality of bend modes
Up: Bent waveguide model
Previous: Bent waveguide model
Contents
Bend mode normalization
The power flow density associated with a bend mode is given by the time
averaged Poynting vector
 . The axial component
. The axial component
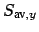 vanishes in the 2-D
setting; for TE waves the radial and azimuthal components evaluate to
vanishes in the 2-D
setting; for TE waves the radial and azimuthal components evaluate to
and for TM polarization one obtains
The total optical power transported by the mode in the angular direction is
given by
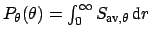 .
Somewhat surprisingly, this expression can be considerably simplified by using
the following formula [89, Section 11.2, Eq. 5],
.
Somewhat surprisingly, this expression can be considerably simplified by using
the following formula [89, Section 11.2, Eq. 5],
where  ,
, 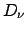 are any cylindrical functions (i.e. functions which
are linear combinations of
J
are any cylindrical functions (i.e. functions which
are linear combinations of
J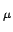 and
Y
and
Y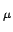 , or of
J
, or of
J and
Y
and
Y , respectively). Observing that for a valid
mode profile the pieces of the ansatz (2.6) satisfy the
polarization dependent continuity conditions at the dielectric interfaces,
application of Eq. (2.11) and of several standard identities for
Bessel functions leads to exact cancellation of the boundary terms that arise
in the piecewise integration, with the exception of the limit term for
, respectively). Observing that for a valid
mode profile the pieces of the ansatz (2.6) satisfy the
polarization dependent continuity conditions at the dielectric interfaces,
application of Eq. (2.11) and of several standard identities for
Bessel functions leads to exact cancellation of the boundary terms that arise
in the piecewise integration, with the exception of the limit term for
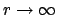 . In that regime the mode profile is represented by the
asymptotic form (2.5) of the relevant Hankel functions, such that
one arrives at the two expressions
. In that regime the mode profile is represented by the
asymptotic form (2.5) of the relevant Hankel functions, such that
one arrives at the two expressions
for the modal power of TE and TM polarized modes, respectively. For certain well guided modes
with extremely low losses, i.e.
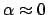 , Eqs. (2.12) are
not suitable for direct use. In this case, we compute the modal power by
numerical integration of
, Eqs. (2.12) are
not suitable for direct use. In this case, we compute the modal power by
numerical integration of
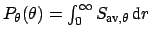 over a suitably chosen radial interval. All mode
profiles shown in Section 2.4 are power normalized with respect to
these expressions (evaluated at
over a suitably chosen radial interval. All mode
profiles shown in Section 2.4 are power normalized with respect to
these expressions (evaluated at  ).
).
Alternatively, Eqs. (2.12) can be derived in a way quite analogous
to what follows in Section 2.2.2: Upon integrating the vanishing
divergence of the Poynting vector
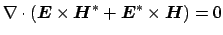 for a modal solution
for a modal solution
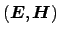 over a
differential angular segment in the domain of polar coordinates, by means of
Gauss' theorem one relates the angular decay of modal power to the outflow of
optical power in the radial direction. The limit of that flow for large radial
coordinates exists and can be evaluated by again using the asymptotic form
(2.5) of the mode profile, leading to expressions
(2.12) for the modal power.
over a
differential angular segment in the domain of polar coordinates, by means of
Gauss' theorem one relates the angular decay of modal power to the outflow of
optical power in the radial direction. The limit of that flow for large radial
coordinates exists and can be evaluated by again using the asymptotic form
(2.5) of the mode profile, leading to expressions
(2.12) for the modal power.
By considering the above expressions for large bend radii, one might wonder
whether these may lead to a scheme for the normalization of nonguided modal
solutions associated with straight waveguides e.g. as given in
[90] in terms of plane wave superpositions. Examination of
Eq. (2.12) with the help of Eq. (2.25), however shows
that the expression (2.12) for the modal power is not applicable in
the limit
 . Hence in this respect, there is no direct
correspondence between the present bend modes supported by structures with low
curvature and radiative modes of similar straight waveguides.
. Hence in this respect, there is no direct
correspondence between the present bend modes supported by structures with low
curvature and radiative modes of similar straight waveguides.




Next: Orthogonality of bend modes
Up: Bent waveguide model
Previous: Bent waveguide model
Contents
Kirankumar Hiremath
2005-09-23
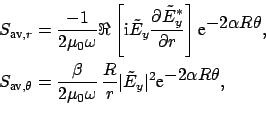
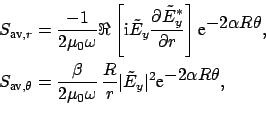
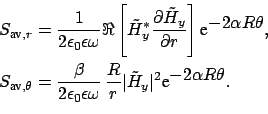
![]() .
Somewhat surprisingly, this expression can be considerably simplified by using
the following formula [89, Section 11.2, Eq. 5],
.
Somewhat surprisingly, this expression can be considerably simplified by using
the following formula [89, Section 11.2, Eq. 5],
![]() for a modal solution
for a modal solution
![]() over a
differential angular segment in the domain of polar coordinates, by means of
Gauss' theorem one relates the angular decay of modal power to the outflow of
optical power in the radial direction. The limit of that flow for large radial
coordinates exists and can be evaluated by again using the asymptotic form
(2.5) of the mode profile, leading to expressions
(2.12) for the modal power.
over a
differential angular segment in the domain of polar coordinates, by means of
Gauss' theorem one relates the angular decay of modal power to the outflow of
optical power in the radial direction. The limit of that flow for large radial
coordinates exists and can be evaluated by again using the asymptotic form
(2.5) of the mode profile, leading to expressions
(2.12) for the modal power.
![]() . Hence in this respect, there is no direct
correspondence between the present bend modes supported by structures with low
curvature and radiative modes of similar straight waveguides.
. Hence in this respect, there is no direct
correspondence between the present bend modes supported by structures with low
curvature and radiative modes of similar straight waveguides.