Propagation constants

For purposes of validating our implementation we start with a comparison of phase propagation constants and attenuation levels. Tables 2.1 and 2.2 list values for angular mode numbers obtained with the present mode solver for two bend configurations adopted from Ref. [43], together with reference data from that source. We found an excellent overall agreement, for both the configurations with higher (Table 2.1) and lower refractive index contrast (Table 2.2).

Table: TE$_{0}$ angular mode numbers $\nu$ for bent waveguides of different bend radius $R$ according to Figure 2.1, with $(n_{\mbox{\scriptsize s}}, n_{\mbox{\scriptsize f}}, n_{\mbox{\scriptsize c}})=(1.6, 1.7, 1.6)$, $d=1\,\mu$m, for a vacuum wavelength $\lambda=1.3\,\mu$m. Second column: Results from Ref. [43].

$R\ [\,\mu$m$]$	$\nu = \gamma' R'$,  Ref. [43]	$\nu = \gamma R$,  present
$50.5$	$4.0189\cdot 10^{2} -$   i$\,7.9990\cdot 10^{-2}$	$4.0189\cdot 10^{2} -$   i$\,7.9973\cdot 10^{-2}$
$100.5$	$8.0278\cdot 10^{2} - ($i$\,1.2856\cdot 10^{-2})$	$8.0278\cdot 10^{2} -$   i$\,9.6032\cdot 10^{-4}$
$150.5$	$1.2039\cdot 10^{3} -$   i$\,7.3948\cdot 10^{-6}$	$1.2039\cdot 10^{3} -$   i$\,7.3914\cdot 10^{-6}$
$200.5$	$1.6051\cdot 10^{3} -$   i$\,4.9106\cdot 10^{-8}$	$1.6051\cdot 10^{3} -$   i$\,4.8976\cdot 10^{-8}$

Table: TE$_{0}$ angular mode numbers $\nu$ for low contrast bends according to Figure 2.1, with different bend radius $R$ and parameters $(n_{\mbox{\scriptsize s}}, n_{\mbox{\scriptsize f}}, n_{\mbox{\scriptsize c}}) = (3.22, 3.26106, 3.22)$, $d=1\,\mu$m, for a vacuum wavelength $\lambda=1.3\,\mu$m. Second column: Results from Ref. [43].

$R\ [\,\mu$m$]$	$\nu = \gamma' R'$,  Ref. [43]	$\nu = \gamma R$,  present
$200.5$	$3.1364\cdot 10^{3} -$   i$\,6.2059\cdot 10^{-1}$	$3.1364\cdot 10^{3} -$   i$\,6.2135\cdot 10^{-1}$
$400.5$	$6.2700\cdot 10^{3} -$   i$\,4.9106\cdot 10^{-2}$	$6.2700\cdot 10^{3} -$   i$\,4.9159\cdot 10^{-2}$
$600.5$	$9.4041\cdot 10^{3} -$   i$\,2.5635\cdot 10^{-3}$	$9.4041\cdot 10^{3} -$   i$\,2.5636\cdot 10^{-3}$
$800.5$	$1.2538\cdot 10^{4} -$   i$\,1.1174\cdot 10^{-4}$	$1.2538\cdot 10^{4} -$   i$\,1.1177\cdot 10^{-4}$
$1000.5$	$1.5673\cdot 10^{4} -$   i$\,4.4804\cdot 10^{-6}$	$1.5673\cdot 10^{4} -$   i$\,7.1806\cdot 10^{-5}$

The discussion of bent waveguides in Ref. [43] applies an alternative definition of the bend radius $R'$ as the distance from the origin to the center of the core layer, which is related to the radius $R$ as introduced in Figure 2.1 by $R'=R-d/2$ (hence the unusual values of bend radii in Tables 2.1, 2.2). Both definitions are meant as descriptions of the same physical configuration, i.e. both lead to the same angular field dependence (2.1), given in terms of the azimuthal mode numbers $\nu$ as determined by the dispersion equation (2.7). Via the relation $\nu = \gamma R = \gamma' R'$, the different choices of the bend radius result in different values $\gamma$ and $\gamma' = \gamma R / (R-d/2)$ for the propagation constant, and consequently in different values $\beta$, $\beta '$ and $\alpha$, $\alpha '$ for the phase and attenuation constants.

Still, for many applications one is interested in the variation of the phase constant and the attenuation with the curvature of the bend, expressed by the bend radius. Figure 2.2 shows corresponding plots for the configuration of Table 2.1, including values for the two different bend radius definitions. While on the scale of the figure the differences are not visible for the attenuation constants, the levels of the phase propagation constants differ indeed substantially for smaller bend radii. As expected, for low curvature the values of both $\beta /k$ and $\beta'/k$ tend to the effective indices of straight slab waveguides with equivalent refractive index profile. For the present low contrast configuration, only minor differences between TE and TM polarization occur.

Figure 2.2: Phase constants $\beta$, $\beta '$ and attenuation constants $\alpha$, $\alpha '$ versus the bend radius $R$, for bends according to Table 2.1. The dashed quantities $\beta ' = \beta R/R'$ and $\alpha ' = \alpha R/R'$ correspond to a description of the bend in terms of an alternative bend radius $R'=R-d/2$. The dotted lines in the first two plots indicate the levels of the effective indices of a straight waveguide with the cross section and refractive index profile of the bent slabs.

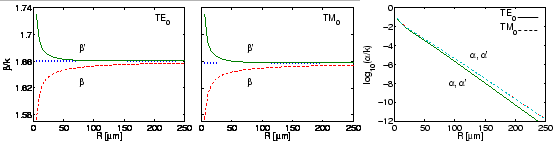Certainly no physical reasoning should rely on the entirely arbitrary definition of the bend radius. This concerns e.g. statements about the growth or decay of phase propagation constants with $R$ (according to Figure 2.2 the sign of the slope can indeed differ), or discussions about the ``phase matching'' of bent waveguides and straight channels in coupler or microresonator configurations. Care must be taken that values for $\beta$ and $\alpha$ or effective quantities like $\beta /k$ are used with the proper definition of $R$ taken into account.

With the present (semi) analytic solutions at hand, we have now a possibility to validate ``classical'' expressions for the variation of the bend attenuation with the bend radius. Beyond the high curvature region, Figure 2.2 shows a strict exponential decay of $\alpha$ with respect to $R$, as predicted by an approximate loss formula for symmetric bent slabs given in [93, Eq. 9.6-24]:

$$\hspace{-0.05cm}\alpha = \frac{R-w}{R}\, \frac{g^{2}}{2 \beta_{\m... ...scriptsize s}}\, \mbox{tanh}^{-1}(g / \beta_{\mbox{\scriptsize s}}) - g)(R-w)}.$$ (2.25)

Here $\beta_{\mbox{\scriptsize s}}$ is the propagation constant corresponding to the straight waveguide with the width $d = 2w$ and refractive index profile $(n_{\mbox{\scriptsize s}}, n_{\mbox{\scriptsize f}}, n_{\mbox{\scriptsize s}})$ of the bent waveguide under investigation. Derived quantities are $g^2 = \beta_{\mbox{\scriptsize s}}^2 - n_{\mbox{\scriptsize s}}^2 k^{2}$ and $h^2 = (n_{\mbox{\scriptsize f}}^{2} - n_{\mbox{\scriptsize s}}^2)k^{2} - g^2$. Figure 2.3 reveals a very good agreement with the attenuation constants calculated by our procedures for bends with low curvature.

Figure: Attenuation constants of the principal TE and TM modes for symmetric bent waveguides with $n_{\mbox{\scriptsize f}} = 1.7$, $n_{\mbox{\scriptsize s}} = n_{\mbox{\scriptsize c}} = 1.6$, $d=1\,\mu$m, $\lambda=1.3\,\mu$m, for varying bend radius $R$. The dashed lines show the exponential decay according to Eq. (2.25); the solid curves are the present analytic mode solver results.