Mode profiles

Beyond the values of the propagation constants, the present analytical mode solver permits to evaluate modal fields for the full range of radial coordinates. Figure 2.4 illustrates normalized profiles for a few fundamental TE bend modes of the configurations considered in Table 2.1.

**Figure:** TE $_{0}$ mode profiles for bends according to the setting of Table 2.1, with different bend radii $R = 200, 50, 10\,\mu$ m. First row: radial dependence of the absolute value (solid line), the real- and imaginary part (dashed and dash-dotted lines), and the phase of the basic electric field component $\tilde{E}_y$ . The profiles are normalized according to Eq. (2.12), with the global phase adjusted such that $\tilde{E}_y(R)$ is real and positive. Second row: snapshots of the propagating bend modes according to Eq. (2.1). The gray scales correspond to the levels of the real, physical field .
$\begin{figure}\begin{center} \epsfig{file=bwg/riap_int.eps,width=\textwidth} \end{center}\vspace{\skipfig}\end{figure}$

One observes the expected effects [93,43]: Bends with large radii

support modes with almost the familiar symmetric, well confined plane profiles of straight symmetric slab waveguides. With decreasing bend radius, the phase profiles of the bend modes become more and more curved. Along with the increasing attenuation, the maximum in the absolute value of the basic electric field shifts towards the outer rim of the bend, and the relative field levels in the exterior region grow. The mode profiles are essentially complex, with oscillatory behaviour of the real- and imaginary parts of the field profiles in the exterior region. The effects of ``bending'' and the lossy nature of the bend modes are illustrated best by the snapshots of the physical fields in the second row of Figure 2.4.

**Figure:** Fundamental TE (left) and TM mode profiles (right) for symmetric bent slabs with $R = 50\,\mu$ m, $\lambda = 1.55\,\mu$ m, $d=1\,\mu$ m, $n_{\mbox{\scriptsize s}} = n_{\mbox{\scriptsize c}} = 1.45$ , and different core refractive indices. As $n_{\mbox{\scriptsize f}}$ is changed from to to , the effective propagation constants $\gamma /k$ change from i $\,9.2077\cdot 10^{-3}$ to i $\,1.1624\cdot 10^{-3}$ to i $\,2.1364\cdot 10^{-7}$ (TE $_{0}$ ), and from i $\,1.0088\cdot 10^{-2}$ to i $\,1.6013\cdot 10^{-3}$ to i $\,9.4104\cdot 10^{-7}$ (TM $_{0}$ ), respectively.
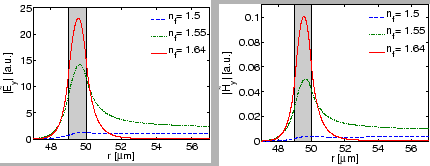$\begin{figure}\begin{center} \epsfig{file=bwg/nc_variation.eps,height=0.3\textwidth} \end{center}\vspace{\skipfig}\end{figure}$

Just as for straight waveguides, the confinement of the bend modes depends critically upon the refractive index contrast. As exemplified by Figure 2.5, one observes quite similar effects when the core refractive index of the bend is varied, as found for the change in bend radius: With loosened confinement and growing attenuation for decreasing $n_{\mbox{\scriptsize f}}$ , the mode profile maximum shifts towards the outer rim, and the relative field levels in the exterior region increase. Note that all (normalizable) mode profiles decay for large radial coordinates according to Eqs. (2.6) and (2.17), despite their appearance in Figs. 2.4 and 2.5 (See the insets in Figs. 2.4, 2.7, 2.9).