



Next: Derivation of coupled mode
Up: Bent-straight waveguide couplers
Previous: Bent-straight waveguide couplers
Contents
Coupled mode equations
For the further procedures, the unknown coefficients 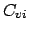 are combined
into amplitude vectors
are combined
into amplitude vectors
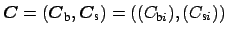 .
To determine equations for these unknowns, here we follow an approach
that relies on a variational principle [111,112]. Consider the
functional
.
To determine equations for these unknowns, here we follow an approach
that relies on a variational principle [111,112]. Consider the
functional
a 2-D restriction of the functional for the 3-D setting given
in [43], stripped from the boundary terms. For the present
2-D configurations, the convention of vanishing derivatives
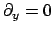 applies to all fields; the curl-operators are to be interpreted accordingly.
applies to all fields; the curl-operators are to be interpreted accordingly.
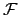 is meant to be viewed as being dependent on the six field
components
is meant to be viewed as being dependent on the six field
components
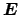 ,
,
 . If
. If 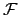 becomes stationary with respect
to arbitrary variations of these arguments, then
becomes stationary with respect
to arbitrary variations of these arguments, then
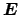 and
and
 satisfy
the Maxwell curl equations as a necessary condition:
satisfy
the Maxwell curl equations as a necessary condition:
We now restrict the functional to the fields allowed by the coupled mode
ansatz. After inserting the trial field (3.3) into the functional
(3.4), 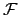 becomes a functional that depends on the
unknown amplitudes
becomes a functional that depends on the
unknown amplitudes
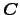 .
For the ``best'' approximation to a solution of the problem
(3.5) in the form of the field (3.3), the
variation of
.
For the ``best'' approximation to a solution of the problem
(3.5) in the form of the field (3.3), the
variation of
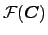 is required to vanish for arbitrary
variations
is required to vanish for arbitrary
variations
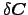 . Disregarding again boundary terms,
the first variations of
. Disregarding again boundary terms,
the first variations of 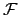 at
at
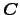 in the directions
in the directions
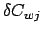 , for
, for
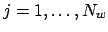 and
and
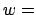 b,s, are
b,s, are
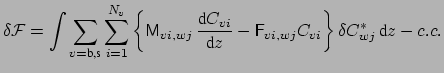 |
(3.6) |
where 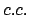 indicates the complex conjugate of the preceding integrated term,
indicates the complex conjugate of the preceding integrated term,
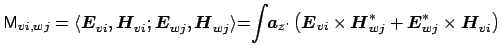 d d |
(3.7) |
and where
 is a unit vector in the
is a unit vector in the 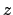 - direction.
Consequently, one arrives at the coupled mode equations
- direction.
Consequently, one arrives at the coupled mode equations
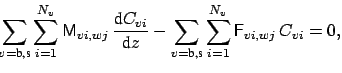 |
(3.9) |
for all
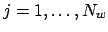 and
and
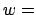 b,s
as a necessary condition for
b,s
as a necessary condition for 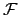 to become stationary
for arbitrary variations
to become stationary
for arbitrary variations
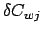 . Note that the same expression
is also obtained from the complex conjugate part of equation (3.6).
In matrix notation, equations (3.9) read
. Note that the same expression
is also obtained from the complex conjugate part of equation (3.6).
In matrix notation, equations (3.9) read
M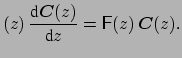 |
(3.10) |
Here the entries of the matrices
M and
F are given by the
integrals (3.7) and (3.8). Due to the functional
form of the bend modes and the varying distance between the bent and straight
cores, these coefficients are 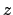 -dependent.
-dependent.
Subsections




Next: Derivation of coupled mode
Up: Bent-straight waveguide couplers
Previous: Bent-straight waveguide couplers
Contents
Kirankumar Hiremath
2005-09-23
![\begin{equation*}\begin{aligned}{\cal{F}(\boldsymbol {E}, \boldsymbol {H})} & = ...
...\boldsymbol {E}^{*} \right] \,\mbox{d}x\,\mbox{d}z, \end{aligned}\end{equation*}](img667.png)