



Next: Coupled mode equations
Up: Bent-Straight waveguide couplers
Previous: Coupled mode theory
Contents
Bent-straight waveguide couplers
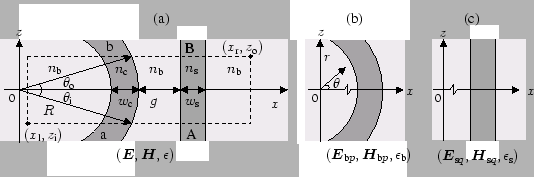
Consider the coupler configuration shown in Figure 3.1(a).
The coupled mode theory description starts with the specification
of the basis fields, here the time-harmonic modal solutions associated with
the isolated bent (b) and straight cores (c). Customarily, the real, positive
frequency 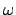 is given by the vacuum wavelength
is given by the vacuum wavelength 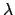 ;
we omit the common time dependence
;
we omit the common time dependence
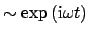 for the sake of brevity. Only forward propagating modes are considered, where,
for convenience, we choose the
for the sake of brevity. Only forward propagating modes are considered, where,
for convenience, we choose the 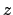 -axis of the Cartesian system as introduced
in Figure 3.1 as the common propagation coordinate for all fields.
-axis of the Cartesian system as introduced
in Figure 3.1 as the common propagation coordinate for all fields.
Figure:
The bent-straight waveguide
coupler setting (a). One assumes that the interaction between the waves supported by
the bent and straight cores is restricted to the rectangular
computational window
![$ [x_{\mbox{\scriptsize l}}, x_{\mbox{\scriptsize r}}] \times [
z_{\mbox{\scriptsize i}}, z_{\mbox{\scriptsize o}}]$](img643.png) . Inside this region the optical field is
represented as a linear combination of the modal fields of the bent
waveguide (b) and of the straight waveguide (c).
. Inside this region the optical field is
represented as a linear combination of the modal fields of the bent
waveguide (b) and of the straight waveguide (c).
 |
Let
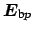 ,
,
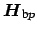 , and
, and
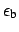 represent the modal electric fields, magnetic fields, and the spatial
distribution of the relative permittivity of the bent waveguide. Due to the
rotational symmetry, these fields are naturally given in the polar coordinate
system
represent the modal electric fields, magnetic fields, and the spatial
distribution of the relative permittivity of the bent waveguide. Due to the
rotational symmetry, these fields are naturally given in the polar coordinate
system  ,
, 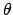 associated with the bent waveguide. For the application
in the CMT formalism, the polar coordinates are expressed in the Cartesian
associated with the bent waveguide. For the application
in the CMT formalism, the polar coordinates are expressed in the Cartesian
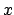 -
-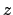 -system, such that the basis fields for the cavity read
-system, such that the basis fields for the cavity read
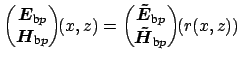 e e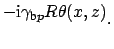 |
(3.1) |
Here
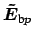 and
and
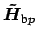 are the
radial dependent electric and magnetic parts of the mode profiles;
the complex propagation constants
are the
radial dependent electric and magnetic parts of the mode profiles;
the complex propagation constants
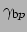 prescribe
the harmonic dependences on the angular coordinate. Note that the actual
values of
prescribe
the harmonic dependences on the angular coordinate. Note that the actual
values of
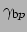 are related to the (arbitrary) definition of
the bend radius
are related to the (arbitrary) definition of
the bend radius 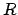 , see Section 2.4.1.
, see Section 2.4.1.
Likewise,
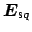 ,
,
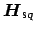 , and
, and
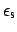 denote the modal fields and the relative permittivity
associated with the straight waveguide. These are of the form
denote the modal fields and the relative permittivity
associated with the straight waveguide. These are of the form
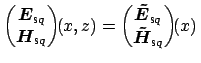 e e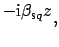 |
(3.2) |
i.e. guided modes with profiles
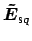 ,
,
 that depend on the lateral coordinate
that depend on the lateral coordinate 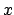 , multiplied by the appropriate
harmonic dependence on the longitudinal coordinate
, multiplied by the appropriate
harmonic dependence on the longitudinal coordinate 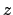 , with
positive propagation constants
, with
positive propagation constants
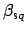 .
Note that for the present 2-D theory all modal
solutions can be computed analytically. While the modal analysis is fairly
standard for straight multilayer waveguides with piecewise constant
permittivity, for the bend structures we employ analytic solutions
in terms of Bessel- and Hankel functions of complex order, computed by means
of a bend mode solver as presented in Chapter 2.
.
Note that for the present 2-D theory all modal
solutions can be computed analytically. While the modal analysis is fairly
standard for straight multilayer waveguides with piecewise constant
permittivity, for the bend structures we employ analytic solutions
in terms of Bessel- and Hankel functions of complex order, computed by means
of a bend mode solver as presented in Chapter 2.
Now the total optical electromagnetic field
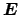 ,
,
 inside the
coupler region is assumed to be well represented by a linear combination of
the modal basis fields (3.1), (3.2),
inside the
coupler region is assumed to be well represented by a linear combination of
the modal basis fields (3.1), (3.2),
 |
(3.3) |
with so far unknown amplitudes 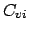 that are allowed to vary with
the propagation coordinate
that are allowed to vary with
the propagation coordinate 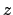 , and
, and
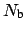 ,
,
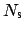 denote
number of bent waveguide and straight waveguide modes under
consideration. This assumption forms the central
approximation of the present CMT approach; no further approximations
or heuristics enter, apart from the numerical procedures used for the
evaluation of the CMT equations (section 3.4). Note that here,
unlike e.g. in Ref. [44], no ``phase matching'' arguments appear;
via the transformation
denote
number of bent waveguide and straight waveguide modes under
consideration. This assumption forms the central
approximation of the present CMT approach; no further approximations
or heuristics enter, apart from the numerical procedures used for the
evaluation of the CMT equations (section 3.4). Note that here,
unlike e.g. in Ref. [44], no ``phase matching'' arguments appear;
via the transformation
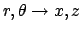 the tilt of the wave
front of the bend modes (3.1) is taken explicitly into account.
the tilt of the wave
front of the bend modes (3.1) is taken explicitly into account.
Subsections




Next: Coupled mode equations
Up: Bent-Straight waveguide couplers
Previous: Coupled mode theory
Contents
Kirankumar Hiremath
2005-09-23


![]() ,
,
![]() , and
, and
![]() represent the modal electric fields, magnetic fields, and the spatial
distribution of the relative permittivity of the bent waveguide. Due to the
rotational symmetry, these fields are naturally given in the polar coordinate
system
represent the modal electric fields, magnetic fields, and the spatial
distribution of the relative permittivity of the bent waveguide. Due to the
rotational symmetry, these fields are naturally given in the polar coordinate
system ![]() ,
, ![]() associated with the bent waveguide. For the application
in the CMT formalism, the polar coordinates are expressed in the Cartesian
associated with the bent waveguide. For the application
in the CMT formalism, the polar coordinates are expressed in the Cartesian
![]() -
-![]() -system, such that the basis fields for the cavity read
-system, such that the basis fields for the cavity read
![]() ,
,
![]() , and
, and
![]() denote the modal fields and the relative permittivity
associated with the straight waveguide. These are of the form
denote the modal fields and the relative permittivity
associated with the straight waveguide. These are of the form
![]() ,
,
![]() inside the
coupler region is assumed to be well represented by a linear combination of
the modal basis fields (3.1), (3.2),
inside the
coupler region is assumed to be well represented by a linear combination of
the modal basis fields (3.1), (3.2),