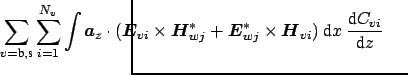Next: Coupled mode equations for
Up: Coupled mode equations
Previous: Coupled mode equations
Contents
Alternatively, the coupled mode equations (3.9) or (3.10) can be
derived by means of a ``reciprocity'' technique [43]. For any two
electromagnetic fields
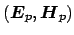 and
and
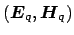 with corresponding relative permittivity distributions
with corresponding relative permittivity distributions
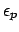 and
and
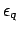 , using the Maxwell equations one can derive
the following identity,
, using the Maxwell equations one can derive
the following identity,
commonly known as ``reciprocity identity'' or ``Lorentz reciprocity
theorem''.
Apply Eq. (3.11) for
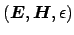 and
and
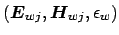 . After straightforward manipulations with the
coupled mode field ansatz (3.3) leads to
. After straightforward manipulations with the
coupled mode field ansatz (3.3) leads to
 i i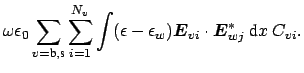 |
(3.12) |
By applying the ``reciprocity identity'' for the second term on the left hand
side of Eq.(3.12), and combining it with the right hand side, one
obtains
 i i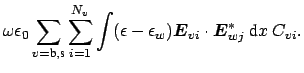 |
(3.13) |
Rewriting Eq. (3.13) in terms of the coefficients
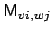 ,
,
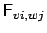 given by Eqs. (3.7), (3.8)
leads to the coupled mode equations (3.9).
given by Eqs. (3.7), (3.8)
leads to the coupled mode equations (3.9).




Next: Coupled mode equations for
Up: Coupled mode equations
Previous: Coupled mode equations
Contents
Kirankumar Hiremath
2005-09-23
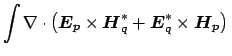 d
d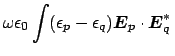 d
d![]() and
and
![]() . After straightforward manipulations with the
coupled mode field ansatz (3.3) leads to
. After straightforward manipulations with the
coupled mode field ansatz (3.3) leads to