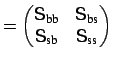Next: Simulation results
Up: Bent-Straight waveguide couplers
Previous: Remarks on the projection
Contents
Reciprocity of scattering matrix
For the analysis of the bent-straight waveguide couplers discussed in
Section 3.2, we have considered only forward propagating modes. By
considering backward propagating modes also, the corresponding full scattering
matrix that relates the bidirectional amplitudes of the outgoing waves to
the amplitudes of the corresponding incoming modes is given as:
 |
(3.21) |
Here the superscripts  indicate the amplitudes of backwards
(anticlockwise) propagating waves, where the zeroes implement
the assumption of negligible backreflections. The entries of the
submatrices
S
indicate the amplitudes of backwards
(anticlockwise) propagating waves, where the zeroes implement
the assumption of negligible backreflections. The entries of the
submatrices
S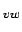 with
with
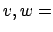 b, s represent the
``coupling'' from the modes of waveguide
b, s represent the
``coupling'' from the modes of waveguide 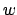 to the fields supported by
waveguide
to the fields supported by
waveguide 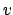 .
.
A fundamental property of any linear optical circuit made of nonmagnetic
materials is that the transmission between any two ``ports'' does not depend
upon the propagation direction. The proof can be based e.g. on the
integration of a reciprocity identity over the spatial domain covered by that
circuit [43]. More specifically, the full scattering matrix of the
reciprocal circuit has to be symmetric. The argument holds for circuits with
potentially attenuating materials, in the presence of radiative losses, and
irrespectively of the particular shape of the connecting cores. It relies
crucially on the precise definition of the ``ports'' of the circuit, where
independent ports can be realized either by mode orthogonality or by spatially
well separated outlets.
Assuming that the requirements of that argument can be applied at least
approximately to our present bent-straight waveguide couplers, one expects
that the coupler scattering matrix is symmetric. For the submatrices
this implies the following equalities (T denotes the transpose):
S |
(3.22) |
If the coupler shown in Figure 3.1 is defined symmetrical with
respect to the central plane 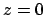 and if identical mode profiles are used for
the incoming and outgoing fields, then one can further expect (see
[43]) the transmission
and if identical mode profiles are used for
the incoming and outgoing fields, then one can further expect (see
[43]) the transmission
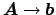 to be equal to the
transmission
to be equal to the
transmission
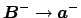 . Similarly, one expects equal
transmissions
. Similarly, one expects equal
transmissions
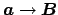 and
and
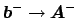 , or
, or
S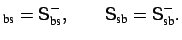 |
(3.23) |
Consequently, according to equations (3.22) and (3.23), also the
unidirectional scattering matrix
S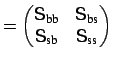 |
(3.24) |
associated with the forward, clockwise propagation through the coupler,
i.e. the lower left quarter block of the full matrix in equation (3.21)
can be expected to be symmetric:
S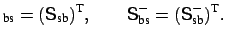 |
(3.25) |
Here translated to the multimode coupler setting, this means that ``the
coupling from the straight waveguide to the cavity bend is equal to the
coupling from the cavity bend to the bus waveguide''.




Next: Simulation results
Up: Bent-Straight waveguide couplers
Previous: Remarks on the projection
Contents
Kirankumar Hiremath
2005-09-23

![]() and if identical mode profiles are used for
the incoming and outgoing fields, then one can further expect (see
[43]) the transmission
and if identical mode profiles are used for
the incoming and outgoing fields, then one can further expect (see
[43]) the transmission
![]() to be equal to the
transmission
to be equal to the
transmission
![]() . Similarly, one expects equal
transmissions
. Similarly, one expects equal
transmissions
![]() and
and
![]() , or
, or