Subsequently, a standard fourth order Runge-Kutta scheme [113] serves
to generate a numerical solution of the coupled mode equations
over the computational domain
![]() , which is split
into intervals of equal length
, which is split
into intervals of equal length ![]() . Exploiting the linearity of equation
(3.10), the procedure is formulated directly for the transfer matrix
T, i.e. applied to the matrix equation
. Exploiting the linearity of equation
(3.10), the procedure is formulated directly for the transfer matrix
T, i.e. applied to the matrix equation
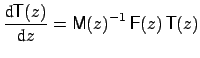 |
(3.26) |
Having explained how to compute the scattering matrices for the bent-straight waveguide couplers, in Section 3.4.1 and 3.4.2 we summarize a series of numerical results for the theory outlined in Section 3.2 and 3.3. Note that couplers with quite small radius with substantial refractive index contrast are considered as test structures. For the CMT approach, these represent rather extreme configurations, partially with strongly leaky fields, thus with relatively large field strengths in the regions where the CMT ansatz-field clearly violates the Maxwell equations. One expects that for couplers that consist of bent waveguides with large radii, i.e. with better confined bend modes, and more adiabatic interaction in the coupler regions, the CMT approach comes even closer to reality.