



Next: Spectrum evaluation
Up: Microresonators
Previous: Abstract microresonator model
Contents
Treating the resonator shown in Figure 4.1 as a black box with
four external ports A, B,
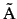 ,
,
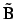 , let's assume that the response of the resonator is
characterized by an abstract bidirectional resonator scattering
matrix
, let's assume that the response of the resonator is
characterized by an abstract bidirectional resonator scattering
matrix
 . Let
. Let
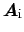 ,
,
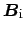 ,
,
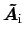 ,
,
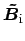 be the amplitudes of
incoming fields, and
be the amplitudes of
incoming fields, and
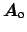 ,
,
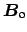 ,
,
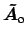 ,
,
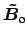 be the outgoing field
amplitudes at the respective ports. Then one can write
be the outgoing field
amplitudes at the respective ports. Then one can write
 |
(4.5) |
where the zeros represent negligible backreflections. The interpretation of
the scattering matrix elements is as for the bent-straight waveguide coupler
(see Section 3.3).
Again following the reciprocity arguments for linear circuits made of
nonmagnetic materials (see Section 3.3), the above
scattering matrix is symmetric, i.e.
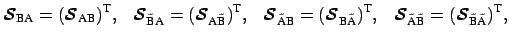 |
(4.6) |
where the superscript T represents the transpose.
If the resonator shown in Figure 4.1 is defined symmetrical with respect to the central plane 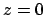 , and if identical mode profiles are used for
the incoming and outgoing fields, then one can further expect the transmission
, and if identical mode profiles are used for
the incoming and outgoing fields, then one can further expect the transmission
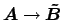 to be equal to the transmission
to be equal to the transmission
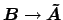 . Similarly, one
expects equal transmissions
. Similarly, one
expects equal transmissions
 and
and
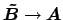 . Therefore one has
. Therefore one has
 |
(4.7) |
From Eq. (4.6), (4.7), one obtains
In case of monomodal port waveguides, this simplifies to
which means that, irrespective of different separation distances, as long as
there is a symmetry with respect to the 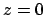 plane, the output power at port
plane, the output power at port
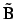 for unit power input at port A and no input at
port
for unit power input at port A and no input at
port
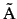 is exactly the same as the power observed at port
B for unit power input at port
is exactly the same as the power observed at port
B for unit power input at port
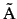 and no input at
port A.
and no input at
port A.
In Section 4.5.3 we show that the numerical implementation
respects these abstract constraints.




Next: Spectrum evaluation
Up: Microresonators
Previous: Abstract microresonator model
Contents
Kirankumar Hiremath
2005-09-23


![]() , and if identical mode profiles are used for
the incoming and outgoing fields, then one can further expect the transmission
, and if identical mode profiles are used for
the incoming and outgoing fields, then one can further expect the transmission
![]() to be equal to the transmission
to be equal to the transmission
![]() . Similarly, one
expects equal transmissions
. Similarly, one
expects equal transmissions
![]() and
and
![]() . Therefore one has
. Therefore one has