Abstract microresonator model

Referring to the classification of resonator types given in [53], we treat the circular microcavities as traveling wave resonators in the framework of a pure frequency domain description. Neglecting reflected waves turns out to be adequate even for the present devices with already quite small radii (though we can check this only implicitly via comparison to numerical results). One expects this approximation to break down for even smaller cavities, where the interaction between the waves in the bus waveguides and the cavity can no longer be regarded as adiabatic. In that regime of standing wave resonators descriptions similar to those given in Refs. [53,115] would have to be applied, that take reflected waves fully into account.

The resonators investigated in this chapter consist of ring or disk shaped dielectric cavities, evanescently coupled to two parallel straight bus cores. We consider guided-wave scattering problems in the frequency domain, where a time-harmonic optical signal $\sim \exp($i$\omega t)$ of given real frequency $\omega$ is present everywhere. Cartesian coordinates $x$, $z$ are introduced for the spatially two dimensional description as shown in Figure 4.1. The structure and all TE- or TM-polarized optical fields are assumed to be constant in the $y$-direction.

Figure 4.1: Schematic microresonator representation: A cavity of radius $R$, core refractive index $n_{\mbox{\scriptsize c}}$ and width $w_{\mbox{\scriptsize c}}$ is placed between two straight waveguides with core refractive index $n_{\mbox{\scriptsize s}}$ and width $w_{\mbox{\scriptsize s}}$, with gaps of width $g$ and $\tilde{g}$ between the cavity and the bus waveguides. $n_{\mbox{\scriptsize b}}$ is the background refractive index. The device is divided into two couplers (I), (II), connected by cavity segments of lengths $L$ and $\tilde{L}$ outside the coupler regions.

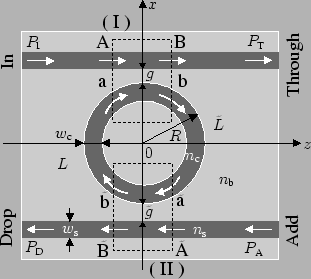Adhering to the most common description for microring-resonators [35,34], the devices are divided into two bent-straight waveguide couplers, which are connected by segments of the cavity ring. Half-infinite pieces of straight waveguides constitute the external connections, where the letters A, B, $\tilde{\mbox{A}}$, $\tilde{\mbox{B}}$ (external) and a, b, $\tilde{\mbox{a}}$, $\tilde{\mbox{b}}$ (internal) denote the coupler ports. If one accepts the approximation that the interaction between the optical waves in the cavity and in the bus waveguides is negligible outside the coupler regions, then this functional decomposition reduces the microresonator description to the mode analysis of straight and bent waveguides, and the modeling of the bent-straight waveguide couplers.

Assuming that all transitions inside the coupler regions are sufficiently smooth, such that reflections do not play a significant role for the resonator functioning, we further restrict the model to unidirectional wave propagation, as indicated by the arrows in Figure 4.1. Depending on the specific configuration, this assumption can be justified or not; at least for the structures considered in Section 4.4.2 we observed this approximation to be adequate.

Consider coupler (I) first. Suppose that the straight cores support $N_{\mbox{\scriptsize s}}$ guided modes with propagation constants $\beta_{\mbox{\scriptsize s}q}$, $q = 1,\ldots,N_{\mbox{\scriptsize s}}$. For the cavity, $N_{\mbox{\scriptsize b}}$ bend modes are taken into account. Due to the radiation losses, their propagation constants $\gamma_{\mbox{\scriptsize b}p} = \beta_{\mbox{\scriptsize b}p} - \mbox{i}\alpha_{\mbox{\scriptsize b}p}$, $p = 1,\ldots,N_{\mbox{\scriptsize b}}$, are complex valued [114]. Here $\beta_{\mbox{\scriptsize s}q}$, $\beta_{\mbox{\scriptsize b}p}$ and $\alpha_{\mbox{\scriptsize b}p}$ are real positive numbers. The variables $A_{q}$, $B_{q}$, and $a_{p}$, $b_{p}$, denote the directional amplitudes of the properly normalized ``forward'' propagating (clockwise direction, cf. Figure 4.1) basis modes in the respective coupler port planes, combined into amplitude (column) vectors $\boldsymbol {A}$, $\boldsymbol {B}$, and $\boldsymbol {a}$, $\boldsymbol {b}$. A completely analogous reasoning applies to the second coupler, where a symbol $\tilde{~}$ identifies the mode amplitudes $\boldsymbol {\tilde{A}}$, $\boldsymbol {\tilde{B}}$, and $\boldsymbol {\tilde{a}}$, $\boldsymbol {\tilde{b}}$ at the port planes.

The model of Chapter 3 for unidirectional wave propagation through the coupler regions provides scattering matrices S, $\tilde{\mbox{\sf {S}}}$, such that the coupler operation is represented as

$$\begin{pmatrix}\boldsymbol {b} \\ \boldsymbol {B} \end{pmatrix} = \begin{pmatrix}\boldsymbol {a} \\ \boldsymbol {A} \end{pmatrix}, ... ...begin{pmatrix}\boldsymbol {\tilde{a}} \\ \boldsymbol {\tilde{A}} \end{pmatrix}.$$ (4.1)

Outside the coupler regions the bend modes used for the description of the field in the cavity propagate independently, with the angular / arc-length dependence given by their propagation constants (cf. equation (3.1)). Hence the amplitudes at the entry and exit ports of the connecting cavity segments are related to each other as

$$\boldsymbol {a} = \,\boldsymbol {\tilde{b}} \quad \boldsymbol {\tilde{a}} = \tilde{\mbox{\sf {G}}}\,\boldsymbol {b},$$ (4.2)

where G and $\tilde{\mbox{\sf {G}}}$ are $N_{\mbox{\scriptsize b}} \times N_{\mbox{\scriptsize b}}$ diagonal matrices with entries ${\sf {G}}_{p,p}=\exp{(-\mbox{i}\gamma_{\mbox{\scriptsize b}p} L)}$ and $\tilde{\sf {G}}_{p,p}=\exp{(-\mbox{i}\gamma_{\mbox{\scriptsize b}p} \tilde{L})}$, respectively, for $p = 1,\ldots,N_{\mbox{\scriptsize b}}$.

For the guided wave scattering problem, modal powers $P_{\mbox{\scriptsize I} q} = \vert A_{q}\vert^2$ and $P_{\mbox{\scriptsize A} q}= \vert\tilde{A}_{q}\vert^2$ are prescribed at the In-port A and at the Add-port $\tilde{\mbox{A}}$ of the resonator, and one is interested in the transmitted powers $P_{\mbox{\scriptsize T}q} = \vert B_{q}\vert^2$ at port B and the backward dropped powers $P_{\mbox{\scriptsize D}q} = \vert\tilde{B}_{q}\vert^2$ at port $\tilde{\mbox{B}}$. The linear system established by equations (4.1) and (4.2) is to be solved for $\boldsymbol {B}$ and $\boldsymbol {\tilde{B}}$, given values of $\boldsymbol {A}$ and $\boldsymbol {\tilde{A}}$. Due to the linearity of the device the restriction to an excitation in only one port, here port A, with no incoming Add-signal $\boldsymbol {\tilde{A}}=\boldsymbol {0}$, is sufficient. One obtains

$$\boldsymbol {B} = ( _{\mbox{\scriptsize sb}} \mbox{\sf {G}} \tilde{\mbox{\sf {S}}}_{\... ...x{\sf {G}}} \Omega^{-1} \mbox{\sf {S}}_{\mbox{\scriptsize bs}}) \boldsymbol {A}$$ (4.3)

for the amplitudes of the outgoing guided modes in the Through- and Drop-ports, and

$$\boldsymbol {b} = \Omega^{-1} _{\mbox{\scriptsize bs}} \boldsymbol {A}, \qquad \boldsymbol {\ti... ...ox{\sf {G}}} \Omega^{-1} \mbox{\sf {S}}_{\mbox{\scriptsize bs}} \boldsymbol {A}$$ (4.4)

for the internal mode amplitudes in the cavity, where $\Omega =$   I$-$   S$_{\mbox{\scriptsize bb}} \mbox{\sf {G}} \tilde{\mbox{\sf {S}}}_{\mbox{\scriptsize bb}} \tilde{\mbox{\sf {G}}}$.

Among the factors in the expressions (4.3) and (4.4) only the inverse of $\Omega$ can be expected to introduce a pronounced wavelength dependence. Thus $\Omega^{-1}$ can be viewed as a resonance denominator in matrix form; resonances appear in case $\Omega$ becomes nearly singular, i.e. exhibits an eigenvalue close to zero. This ``resonance condition'' permits a quite intuitive interpretation: Resonances appear if a field amplitude vector is excited inside the cavity, that corresponds to a close-to-zero eigenvalue of $\Omega$, or a unit eigenvalue of S$_{\mbox{\scriptsize bb}} \mbox{\sf {G}} \tilde{\mbox{\sf {S}}}_{\mbox{\scriptsize bb}} \tilde{\mbox{\sf {G}}}$. That relates to a field which reproduces itself after propagating consecutively along the right cavity segment, through coupler (II), along the left cavity segment, and finally through coupler (I).

In general, resonances must be expected to involve all bend modes that are taken into account for the description of the cavity field, due to the interaction caused by the presence of the straight cores (cf. e.g. the example of the hybrid cavity ring given in Ref. [69]). If, however, this direct interaction between the bend modes is weak, the matrices S$_{\mbox{\scriptsize bb}}$ and $\tilde{\mbox{\sf {S}}}_{\mbox{\scriptsize bb}}$ become nearly diagonal just like G and $\tilde{\mbox{\sf {G}}}$, and resonances can be ascribed to individual cavity modes. Analogously to the case of standing wave resonators [115], this viewpoint allows a quantitative characterization of resonances associated with ``almost isolated'' cavities, where the bus waveguides are absent. Also for the numerical examples in Section 4.4.2 we found this regime to be realized; resonances can be classified as belonging to specific bend modes by inspecting the mode amplitudes that establish inside the cavity at the resonance wavelength.

In case of a configuration with single mode cavity and bus cores, further evaluation of expressions (4.3) and (4.4) is presented in Section 1.4; one obtains the familiar explicit, parameterized expressions for the transmitted and dropped power, for the free spectral range and the resonance width, for finesse and Q-factor of the resonances, etc. Here the above resonance condition means that at coupler (I) the incoming signal from the bus waveguide is in phase with the wave propagating already along the cavity, and that it compensates the propagation loss of the cavity round trip. Resonances appear as a drop in the directly transmitted power $P_{\mbox{\scriptsize T}}$, and a simultaneous peak in the dropped power $P_{\mbox{\scriptsize D}}$. Assuming that this reasoning is also applicable to a multimode configuration with weak interaction, one can establish separate resonance conditions for the individual cavity modes, which in general will be satisfied at different wavelengths. The power spectrum of the microresonator shows a systematically repeating pattern with multiple extrema, where each resonance corresponds to cavity modes of different orders. See Figure 4.9 for an example.