Microring resonator

For all subsequent computations of microresonator spectra, unless stated explicitly, we restrict ourselves to symmetric structures ( $g=\tilde{g}$) with identical monomodal straight waveguides. In line with the assumptions leading to equations (4.3), (4.4), the fundamental mode of the bus waveguides is launched at the In-port with unit power; there is no incoming field at the Add-port.

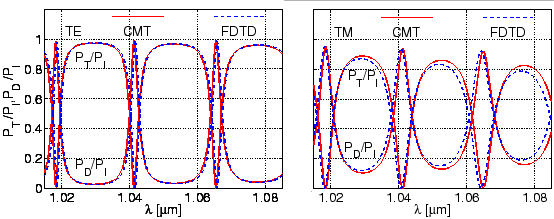
Figure 4.2 shows the spectral response for a microring-resonator made of two couplers as considered in Section 3.4.1, with cavity radius $R=5 \,\mu$m and gaps $g=\tilde{g}= 0.2\,\mu$m. The CMT calculations use the computational setting as introduced for Figure 3.3. One observes the familiar ringresonator resonance pattern with dips in the transmitted power and peaks in the dropped intensity. According to Figure 3.4, the present parameter set specifies configurations with rather strong interaction in the coupler regions ( $\vert{\sf {S}}_{\mbox{\scriptsize b0}, \mbox{\scriptsize s0}}\vert^2 = 30\%$ (TE), $\vert{\sf {S}}_{\mbox{\scriptsize b0}, \mbox{\scriptsize s0}}\vert^2 = 54\%$ (TM)), such that the resonances are relatively wide, with a substantial amount of optical power being directly transferred to the Drop port also in off resonant states. These properties are related to the attenuation of the cavity modes, and to the interaction strength in the coupler regions, i.e. to the radial confinement of the bend fields, hence one finds resonances of lower quality for TM polarization, and a decrease in quality with growing wavelength for both TE and TM polarized light.

Figure: Relative transmitted $P_{\mbox{\scriptsize T}}$ and dropped power $P_{\mbox{\scriptsize D}}$ versus the vacuum wavelength for a ringresonator according to Figure 4.1, with parameters $n_{\mbox{\scriptsize c}}= n_{\mbox{\scriptsize s}}=1.5$, $n_{\mbox{\scriptsize b}}=1.0$, $w_{\mbox{\scriptsize c}}=0.5\,\mu\mbox{m}$, $w_{\mbox{\scriptsize s}} = 0.4\,\mu\mbox{m}$, $R=5 \,\mu$m, $g=\tilde{g}= 0.2\,\mu$m; CMT and FDTD results for TE (left) and TM polarization (right).

The CMT results are compared with FDTD simulations, where a computational window that encloses the entire resonator device has been discretized by a rectangular grid of $1200 \times 1220$ points along the $x$- and $z$-directions with uniform mesh size of $0.0125\,\mu$m. The boundaries of the computational window are enclosed by $0.4 \,\mu$m wide perfectly matched layers with quadratically varying strength, which provide a reflectivity of $10^{-6}$ for the central wavelength $\lambda=1.05\,\mu$m. The simulations are carried out over a time interval of $13.1\,$ps with a step size of $0.025\,$fs. According to the left and right plots of Figure 4.2, we find an excellent agreement between the CMT and the FDTD results for TE polarization, and only minor deviations for the TM case with less regular fields, more pronounced radiation, and stronger interaction in the coupler regions, where apparently the assumptions underlying the CMT approach are less well satisfied. Note that already in the present 2-D setting these FDTD calculations typically require a computation time of several hours, while the CMT analysis (with interpolation) predicts the entire spectrum in just a few minutes.