2D bent-straight waveguide couplers simulator

Bent-straight waveguide couplers are one of the ingredients of the "standard model" of circular microresonators. The response of these couplers is characterized by scattering matrices, which in turn determine the spectral response of the resonators. Therefore it is essential to have a parameter free model of bent-straight waveguide couplers.

Capitalizing on the availability of rigorous analytical modal solutions for 2-D bent waveguides, these couplers are modeled using a frequency domain spatial coupled mode formalism, derived by means of a variational principle or reciprocity technique.

Here, we analyze the interaction between bent waveguides and straight waveguides in two dimensional settings, using spatial coupled mode theory. The formulation presented in here takes into account that multiple modes in each of the cores may turn out to be relevant for the functioning of the resonators. Having access to analytical 2-D bend modes proves useful for the numerical implementation of this model.

Bend-straight waveguide couplers model

Consider the coupler configuration shown in Figure 1(a). The coupled mode theory description starts with the specification of the basis fields, here the time-harmonic modal solutions associated with the isolated bent (b) and straight cores (c). Customarily, the real, positive frequency $ \omega$ is given by the vacuum wavelength $ \lambda$; we omit the common time dependence $ \sim \exp{(\mbox{i}\omega t)}$ for the sake of brevity. Only forward propagating modes are considered, where, for convenience, we choose the $ z$-axis of the Cartesian system as introduced in Figure 1 as the common propagation coordinate for all fields.

Figure 1: The bent-straight waveguide coupler setting (a). One assumes that the interaction between the waves supported by the bent and straight cores is restricted to the rectangular computational window $ [x_{\mbox{\scriptsize l}}, x_{\mbox{\scriptsize r}}] \times [ z_{\mbox{\scriptsize i}}, z_{\mbox{\scriptsize o}}]$. Inside this region the optical field is represented as a linear combination of the modal fields of the bent waveguide (b) and of the straight waveguide (c).

Let $ \boldsymbol {E}_{\mbox{\scriptsize b}p}$, $ \boldsymbol {H}_{\mbox{\scriptsize b}p}$, and $ \epsilon_{\mbox{\scriptsize b}}$ represent the modal electric fields, magnetic fields, and the spatial distribution of the relative permittivity of the bent waveguide. Due to the rotational symmetry, these fields are naturally given in the polar coordinate system $ r$, $ \theta$ associated with the bent waveguide. For the application in the CMT formalism, the polar coordinates are expressed in the Cartesian $ x$-$ z$-system, such that the basis fields for the cavity read

$\displaystyle \begin{pmatrix}\boldsymbol {E}_{\mbox{\scriptsize b}p} \\ \boldsy... ...boldsymbol {\tilde{H}}_{\mbox{\scriptsize b}p} \end{pmatrix}\!\!(r(x, z)) \,$e$\displaystyle ^{\displaystyle -\mbox{i}\gamma_{\mbox{\scriptsize b}p} R \theta(x, z)}.$ (1)

Here $ \boldsymbol {\tilde{E}}_{\mbox{\scriptsize b}p}$ and $ \boldsymbol {\tilde{H}}_{\mbox{\scriptsize b}p}$ are the radial dependent electric and magnetic parts of the mode profiles; the complex propagation constants $ \gamma_{\mbox{\scriptsize b}p}$ prescribe the harmonic dependences on the angular coordinate. Note that the actual values of $ \gamma_{\mbox{\scriptsize b}p}$ are related to the (arbitrary) definition of the bend radius $ R$.

Likewise, $ \boldsymbol {E}_{\mbox{\scriptsize s}q}$, $ \boldsymbol {H}_{\mbox{\scriptsize s}q}$, and $ \epsilon_{\mbox{\scriptsize s}}$ denote the modal fields and the relative permittivity associated with the straight waveguide. These are of the form

$\displaystyle \begin{pmatrix}\boldsymbol {E}_{\mbox{\scriptsize s}q}\\ \boldsym... ...s}q}\\ \boldsymbol {\tilde{H}}_{\mbox{\scriptsize s}q}\end{pmatrix}\!\!(x) \,$e$\displaystyle ^{\displaystyle -\mbox{i}\beta_{\mbox{\scriptsize s}q} z},$ (2)

i.e. guided modes with profiles $ \boldsymbol {\tilde{E}}_{\mbox{\scriptsize s}q}$, $ \boldsymbol {\tilde{H}}_{\mbox{\scriptsize s}q}$ that depend on the lateral coordinate $ x$, multiplied by the appropriate harmonic dependence on the longitudinal coordinate $ z$, with positive propagation constants $ \beta_{\mbox{\scriptsize s}q}$. Note that for the present 2-D theory all modal solutions can be computed analytically. While the modal analysis is fairly standard for straight multilayer waveguides with piecewise constant permittivity, for the bend structures we employ analytic solutions in terms of Bessel- and Hankel functions of complex order, computed by means of a bend mode solver as presented in Ref. [1].

Now the total optical electromagnetic field $ \boldsymbol {E}$, $ \boldsymbol {H}$ inside the coupler region is assumed to be well represented by a linear combination of the modal basis fields (1), (2),

$\displaystyle \begin{pmatrix}\boldsymbol {E}\\ \boldsymbol {H}\end{pmatrix}\!\!... ...begin{pmatrix}\boldsymbol {E}_{vi}\\ \boldsymbol {H}_{vi}\end{pmatrix}\!\!(x,z)$ (3)

with so far unknown amplitudes $ C_{vi}$ that are allowed to vary with the propagation coordinate $ z$, and $ N_{\mbox{\scriptsize b}}$, $ N_{\mbox{\scriptsize s}}$ denote number of bent waveguide and straight waveguide modes under consideration. This assumption forms the central approximation of the present CMT approach; no further approximations or heuristics enter, apart from the numerical procedures used for the evaluation of the CMT equations (see Numerics).

Go to top

Coupled mode equations

For the further procedures, the unknown coefficients $ C_{vi}$ are combined into amplitude vectors $ \boldsymbol {C} = (\boldsymbol {C}_{\mbox{\scriptsize b}}, \boldsymbol {C}_{\mbox{\scriptsize s}}) = ((C_{\mbox{\scriptsize b}i}), (C_{\mbox{\scriptsize s}i}))$. By using a variational principle or Lorentz reciprocity theorem, one gets the following coupled mode equation for these unknowns (see Ref. [2])

$\displaystyle \hspace{-0.1cm} \sum_{v=\mbox{\scriptsize b,s}} \sum_{i=1}^{N_{v... ...v=\mbox{\scriptsize b,s}} \sum_{i=1}^{N_{v}} {\sf {F}}_{vi, wj}\, C_{vi} = 0,$ (4)

for all $ j=1,\ldots,N_{w}$ and $ w=$b,s where,

$\displaystyle {\sf {M}}_{vi,wj} = \langle \boldsymbol {E}_{vi}^{}, \boldsymbol ... ..._{wj}^{*} + \boldsymbol {E}_{wj}^{*} \times \boldsymbol {H}_{vi}^{} \right )\,$d$\displaystyle x,$ (5)

$\displaystyle {\sf {F}}_{vi,wj} = -$   i$\displaystyle \omega \epsilon_{0} \int (\epsilon - \epsilon_{v}) \boldsymbol {E}_{vi}^{} \cdot \boldsymbol {E}_{wj}^{*}\,$d$\displaystyle x,$ (6)

and where $ \boldsymbol {a}_{z}$ is a unit vector in the $ z$- direction.

In matrix notation, equations (4) read

M$\displaystyle (z)\, \frac{\mbox{d}\boldsymbol {C}(z)}{\mbox{d}z} = \mbox{\sf {F}}(z)\,\boldsymbol {C}(z).$ (7)

Here the entries of the matrices M and F are given by the integrals (5) and (6). Due to the functional form of the bend modes and the varying distance between the bent and straight cores, these coefficients are $ z$-dependent.

Coupled mode equations for couplers with monomodal waveguides

In the single mode case $ N_{\mbox{\scriptsize b}}= N_{\mbox{\scriptsize s}} = 1$, Eq.(7) is given explicitely [3, 4] as

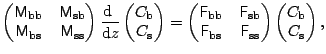$\displaystyle \begin{pmatrix} {\sf {M}}_{\mbox{\scriptsize bb}} & {\sf {M}}_{\... ...gin{pmatrix}C_{\mbox{\scriptsize b}} \\ C_{\mbox{\scriptsize s}} \end{pmatrix},$ (8)

where the mode index $ p=q=1$ is omitted for simplicity.



Go to top

Transfer matrix and scattering matrix

Transfer matrix

To proceed further, the coupled mode equations are solved by numerical means; the result can be stated in terms of a transfer matrix T that relates the CMT amplitudes at the output plane $ z= z_{\mbox{\scriptsize o}}$ to the amplitudes at the input plane $ z=z_{\mbox{\scriptsize i}}$ of the coupler region:

$\displaystyle \boldsymbol {C}(z_{\mbox{\scriptsize o}}) = \mbox{\sf {T}}\,\boldsymbol {C}(z_{\mbox{\scriptsize i}}).$ (9)

It remains to relate the transfer matrix, obtained directly as the solution of the CMT equations on the limited computational window, to the coupler scattering matrix as required for the abstract model of resonator [2].

Scattering matrix

Outside the coupler (i.e. outside the region $ [x_{\mbox{\scriptsize l}}, x_{\mbox{\scriptsize r}}] \times [ z_{\mbox{\scriptsize i}}, z_{\mbox{\scriptsize o}}]$), it is assumed that the interaction between the fields associated with the different cores is negligible. The individual modes propagate undisturbed according to the harmonic dependences on the respective propagation coordinates, such that the external fields are:

(10)

and

\begin{equation*}\begin{aligned} b_{p} \begin{pmatrix} \boldsymbol {\tilde{E... ... \mbox{~for~} z \geq z_{\mbox{\scriptsize o}}. \end{aligned}\end{equation*}
(11)

Here $ \boldsymbol {a}=(a_{p})$, $ \boldsymbol {A}=(A_{q})$ and $ \boldsymbol {b}=(b_{p})$, $ \boldsymbol {B}=(B_{q})$ are the constant external mode amplitudes at the input and output ports of the coupler. See Figure 1 for the definitions of the coordinate offsets $ z_{\mbox{\scriptsize i}}$, $ \theta_{\mbox{\scriptsize i}}$ and $ z_{\mbox{\scriptsize o}}$, $ \theta_{\mbox{\scriptsize o}}$.

For a typical coupler configuration, the guided modal fields of the straight waveguide are well confined to the straight core. On the contrary, due to the radiative nature of the fields, the bend mode profiles can extend far beyond the outer interface of the bent waveguide. Depending upon the specific physical configuration, the extent of these radiative parts of the fields varies, such that also outside the actual coupler region, the field strength of the bend modes in the region close to the straight core may be significant. Therefore, to assign the external mode amplitudes $ A_q$, $ B_q$, it turns out to be necessary to project the coupled field on the straight waveguide modes.

At a sufficient distance from the cavity, in the region where only the straight waveguide is present, the total field $ \phi = (\boldsymbol {E}, \boldsymbol {H})$ can be expanded into the complete set of modal solutions of the eigenvalue problem for the straight waveguide. The basis set consists of a finite number of guided modes $ \phi_{\mbox{\scriptsize s}q} = (\boldsymbol {E}_{\mbox{\scriptsize s}q}, \boldsymbol {H}_{\mbox{\scriptsize s}q})$ and a nonguided, radiative part $ \phi_{\mbox{\scriptsize rad}}$, such that

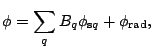$\displaystyle \phi = \sum_{q} B_{q} \phi_{\mbox{\scriptsize s}q} + \phi_{\mbox{\scriptsize rad}},$ (12)

where $ B_{q}$ are the constant amplitudes of $ \phi_{\mbox{\scriptsize s}q}$. These amplitudes can be extracted by applying the formal expansion to the total field (3) as given by the solution of the CMT equations. Using the orthogonality properties of the basis elements, the projection at the output plane $ z= z_{\mbox{\scriptsize o}}$ of the coupler yields

$\displaystyle B_{q} \exp{(\mbox{i}\beta_{\mbox{\scriptsize s}q} z)} = C_{\mbox{... ...box{\scriptsize s}q}}{{\sf {M}}_{\mbox{\scriptsize s}q,\mbox{\scriptsize s}q}}.$ (13)

where the mode overlaps $ \langle \phi_{mi}; \phi_{nj} \rangle = \langle \boldsymbol {E}_{mi}^{}, \bolds... ... ; \boldsymbol {E}_{nj}^{}, \boldsymbol {H}_{nj}^{} \rangle = {\sf {M}}_{mi,nj}$ occur already in the coupled mode equations (7). An expression analogous to (13) can be written for the projection at $ z=z_{\mbox{\scriptsize i}}$, where the coefficients $ A_q$ are involved. What concerns the external amplitudes of the bend modes, no such procedure is required, since the field strength of the straight waveguide modes is usually negligible in the respective angular planes, where the major part of the bend mode profiles is located. Here merely factors are introduced that adjust the offsets of the angular coordinates in (10),(11) .

Thus, given the solution (9) of the coupled mode equations in the form of the transfer matrix T, the scattering matrix S that relates the amplitudes $ a_p$, $ b_p$, $ A_q$, $ B_q$ of the external fields (shown in Figure 1) is defined as

S$\displaystyle =$   Q$\displaystyle \,$T$\displaystyle \,$P$\displaystyle ^{-1}$ (14)

where P and Q are $ (N_{\mbox{\scriptsize b}} + N_{\mbox{\scriptsize s}}) \times (N_{\mbox{\scriptsize b}} + N_{\mbox{\scriptsize s}})$ matrices with diagonal entries $ {\sf {P}}_{p,p}=\exp{(-\mbox{i}\gamma_{\mbox{\scriptsize b}p} R \theta_{\mbox{\scriptsize i}})}$ and $ {\sf {Q}}_{p,p} = \exp{(-\mbox{i}\gamma_{\mbox{\scriptsize b}p} R \theta_{\mbox{\scriptsize o}})}$, for $ p = 1,\ldots,N_{\mbox{\scriptsize b}}$, followed by the entries $ {\sf {P}}_{q+{N_{\mbox{\scriptsize b}}},q+{N_{\mbox{\scriptsize b}}}} = \exp{(-\mbox{i}\beta_{\mbox{\scriptsize s}q} z_{\mbox{\scriptsize i}})}$ and $ {\sf {Q}}_{q+{N_{\mbox{\scriptsize b}}},q+{N_{\mbox{\scriptsize b}}}} = \exp{(-\mbox{i}\beta_{\mbox{\scriptsize s}q} z_{\mbox{\scriptsize o}})}$, for $ q = 1,\ldots,N_{\mbox{\scriptsize s}}$.

A lower left block is filled with entries $ {\sf {P}}_{q+{N_{\mbox{\scriptsize b}}},p} = \exp{(-\mbox{i}\beta_{\mbox{\sc... ...riptsize s}q,\mbox{\scriptsize s}q} \right \vert _{z=z_{\mbox{\scriptsize i}}}$ and $ {\sf {Q}}_{q+{N_{\mbox{\scriptsize b}}},p} = \exp{(-\mbox{i}\beta_{\mbox{\sc... ...criptsize s}q,\mbox{\scriptsize s}q} \right \vert _{z=z_{\mbox{\scriptsize o}}}$, for $ q = 1,\ldots,N_{\mbox{\scriptsize s}}$ and $ p = 1,\ldots,N_{\mbox{\scriptsize b}}$, respectively, that incorporate the projections. All other coefficients of P and Q are zero.

Go to top

Numerics

The coupled mode equations (4), (7) are treated by numerical means on a rectangular computational window as introduced in Figure 1. The solution involves the numerical quadrature of the integrals (5), (6) in the $ z$-dependent matrices M and F, where a simple trapezoidal rule [5] is applied, using an equidistant discretization of $ [x_{\mbox{\scriptsize l}}, x_{\mbox{\scriptsize r}}]$ into intervals of length $ h_x$.

Subsequently, a standard fourth order Runge-Kutta scheme [5] serves to generate a numerical solution of the coupled mode equations over the computational domain $ [z_{\mbox{\scriptsize i}}, z_{\mbox{\scriptsize o}}]$, which is split into intervals of equal length $ h_z$. Exploiting the linearity of equation (7), the procedure is formulated directly for the transfer matrix T, i.e. applied to the matrix equation

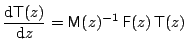$\displaystyle \frac{\mbox{d} \mbox{\sf {T}}(z)}{\mbox{d}z} = \mbox{\sf {M}}(z)^{-1}\,\mbox{\sf {F}}(z)\,\mbox{\sf {T}}(z)$ (15)

with initial condition T$ (z_{\mbox{\scriptsize i}}) = \mbox{\sf {I}}$ (the identity matrix), such that $ \boldsymbol {C}(z) =$   T$ (z)\,\boldsymbol {C}(z_{\mbox{\scriptsize i}})$.

As a result, one gets the required transfer matrix T. By incorporating the projections, then it leads to the required scattering matrix S.

Note



Go to top

Couplers simulator: Implementation

Relevent files

bscoupler.h, bscoupler.c Bent-straight waveguide coupler (More)


Go to top

Couplers simulator: Example

Couplers simulator: Example


Go to top

References

  1. K. R. Hiremath, M. Hammer, S. Stoffer, L. Prkna, and J. Ctyroký.
    Analytic approach to dielectric optical bent slab waveguides.
    Optical and Quantum Electronics, 37(1-3):37-61, January 2005.

  2. K. R. Hiremath, R. Stoffer, and M. Hammer.
    Modeling of circular integrated optical microresonators by 2-D frequency domain coupled mode theory.
    2005.
    (accepted).

  3. R. Stoffer, K. R. Hiremath, and M. Hammer.
    Comparison of coupled mode theory and FDTD simulations of coupling between bent and straight optical waveguides.
    In M. Bertolotti, A. Driessen, and F. Michelotti, editors, Microresonators as building blocks for VLSI photonics, volume 709 of AIP conference proceedings, pages 366-377. American Institute of Physics, Melville, New York, 2004.

  4. M. Hammer, K. R. Hiremath, and R. Stoffer.
    Analytical approaches to the description of optical microresonator devices.
    In M. Bertolotti, A. Driessen, and F. Michelotti, editors, Microresonators as building blocks for VLSI photonics, volume 709 of AIP conference proceedings, pages 48-71. American Institute of Physics, Melville, New York, 2004.

  5. W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery.
    Numerical Recipes in C, 2nd ed.
    Cambridge University Press, 1992.



Go to top