2D bent waveguides semianalytic mode solver
|
2D bent waveguides semianalytic mode solver |
|
Bent waveguides play an important role in photonic integrated circuits. Accurate evaluation of mode profiles, phase propagation constants and attenuation constants of leaky bent modes is very important from a device design point of view.
A sound modal analysis of bent slabs becomes particularly relevant, if the mode profiles are to be employed as basis fields for a description of integrated optical microresonators with circular, ring- or disk-shaped cavities. In a framework of coupled mode theory, an as far as possible analytic representation of the basic field profiles on a radially unbounded domain must be regarded as highly advantageous.
Therefore we followed analytical approach. For a detailed theoretical discussions and numerical examples of this approach, refer to [1].
Here we describe 2D bent mode solver based on the above analytical approach.
The model that we going to describe is in principle applicable for arbitrary multilayer bent waveguides. But here we have implemented only a three layer (substrate, core and cladding) configuration.
Consider a bent slab waveguide with the y-axis as the axis of
symmetry as shown in the following figure. We assume that the material
properties and the fields do not vary in the y -direction. In the
cylindrical coordinate system
(r, y, θ), the functional form (in the usual complex notation) of
the propagating electric field and the magnetic field reads
 |
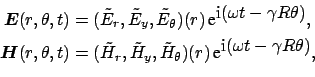
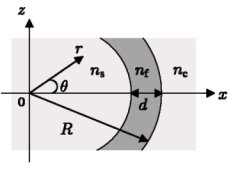Figure 1: A bent slab waveguide. The core of thickness d and refractive index nf is embedded between an interior medium ("substrate") with refractive index ns and an exterior medium ("cladding") with refractive index nc. The distance between the origin and the outer rim of the bend defines the bend radius R. |
By inserting the above ansatz into the Maxwell equations, and rearranging it suitably, one can show that within radial intervals with constant refractive index n, the basic electric and magnetic components are governed by a Bessel equation with complex order γ R,
, and 
, where
k=2π/λ is the (given, real) vacuum wavenumber.
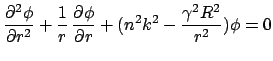
The above Bessel equation is solved piecewise in the regions with constant refractive index, together with the interface conditions and suitable boundary conditions for r=0 and r=∞.
For TE modes, the interface conditions require continuity of
and
across
the dielectric interfaces. For TM modes, continuity of 
and of 
across the interfaces
is required.
In substrate, at origin r=0, field should be finite. In cladding, field should be outgoing and as r tends to ∞, it should decay.
Thus the piecewise ansatz for the basic components of the electric/magnetic bent mode profile is
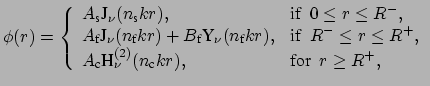
The polarization dependent interface conditions lead to a homogeneous system of linear equations for As, Af, Bf, Ac. The condition for its nontrivial solution lead to the required dispersion equation for bent slab waveguide (see Ref.[1, Eq. 7]). For a given frequency ω, this equation is to be solved for the propagation constants γ = ν /R.
Ordering of modes: Modes of different orders are indexed by counting the local minima in the absolute value of the principal electric (TE) or magnetic (TM) component of the mode profile.
Mode Normalization: The total optical power transported by the mode in the angular direction is given by
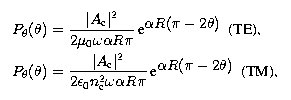
Computation of complex order Bessel functions
To solve the
dispersion equation, one needs the evaluation of Bessel and Hankel functions
of complex order. We have implemented required routines, which are based on
'uniform asymptotic expansions' of Bessel functions and their derivatives in
terms of Airy functions (More).
Root finding of the dispersion equation
As a heuristic search procedure, a suitably selected region of the complex
plane is divided into a number of rectangles, the lower left and upper right
corner points of which are then supplied as initial guesses to a root finding
routine based on the secant method. Repeated roots are rejected, the remaining
unique roots are sorted in descending order of their imaginary part
-α. By refining the subdivision into rectangles, it can be
ascertained with reasonable robustness that all the roots in the given region are captured.
Note: Alternatively, a root tracking procedure can be implemented to
solve the dispersion equation. Starting with the propagation constants of
straight waveguides with a refractive index profile cross section equal to
that of the given bent waveguide, a series of bends with decreasing radius
should be considered, with the roots found for each configuration used as
initial guesses for the subsequent one. In this way, the bend propagation
constants can be followed in the complex plane.
| bmsinc.h | Main header file for bent mode solver |
| bessel.h, bessel.cpp | Routines for computation of (complex order) Bessel functions (More) | dgamma.f, machcon.f, zbsubs.f | Routines for computation of Airy functions (More) |
| bslawaveg.h, bslawaveg.c | Bent slab waveguide definition (More) |
| bslamode.h, bslamode.c | Bent mode definition (More) |
| bslams.h, bslams.c | Bent mode solver (More) |
| bslamarr.h, bslamarr.c | Array of bent modes (More) |
| bslamvis.h, bslamvis.c | Visualisation related routines (More) |
Bent waveguides simulator: Example
|
|
|
|
|
|