2D microresonators simulator

Circular integrated optical microresonators are increasingly employed as compact and versatile wavelength filters. Here we present a 2-D frequency domain simulation tool for these devices.

The resonators are functionally represented in terms of two couplers with appropriate connections using bent and straight waveguides. The abstract scattering matrices of these couplers and the propagation constants of the cavity bends allow to compute the spectral responses of the resonators. These parameters are calculated by means of the rigorous analytical model of bent waveguides, and the spatial coupled mode theory model of the constituent bent-straight waveguide couplers.

Microresonators model: Setting
Microresonators model: Description
Resonators spectral response
Microresonators simulator: Implementation
Microresonators simulator: Example
References

Microresonators model: Setting

The resonators investigated here consist of ring or disk shaped dielectric cavities, evanescently coupled to two parallel straight bus cores. The waveguides are made of linear and nonmagnetic materials. We consider guided-wave scattering problems in the frequency domain, where a time-harmonic optical signal $\sim \exp($ i $\omega t)$ of given real frequency $\omega$ is present everywhere. Cartesian coordinates , are introduced for the spatially two dimensional description as shown in Figure 1. The structure and all TE- or TM-polarized optical fields are assumed to be constant in the -direction.

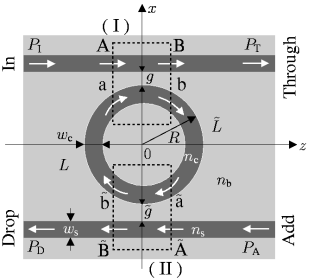
Schematic microresonator representation: A cavity of radius , core refractive index $n_{\mbox{\scriptsize c}}$ and width $w_{\mbox{\scriptsize c}}$ is placed between two straight waveguides with core refractive index $n_{\mbox{\scriptsize s}}$ and width $w_{\mbox{\scriptsize s}}$ , with gaps of width and $\tilde{g}$ between the cavity and the bus waveguides. $n_{\mbox{\scriptsize b}}$ is the background refractive index. The device is divided into two couplers (I), (II), connected by cavity segments of lengths and $\tilde{L}$ outside the coupler regions.

Adhering to the most common description for microring-resonators [2,3], the devices are divided into two bent-straight waveguide couplers, which are connected by segments of the cavity ring. Half-infinite pieces of straight waveguides constitute the external connections, where the letters A, B, $\tilde{\mbox{A}}$ , $\tilde{\mbox{B}}$ (external) and a, b, $\tilde{\mbox{a}}$ , $\tilde{\mbox{b}}$ (internal) denote the coupler ports. If one accepts the approximation that the interaction between the optical waves in the cavity and in the bus waveguides is negligible outside the coupler regions, then this functional decomposition reduces the microresonator description to the mode analysis of straight and bent waveguides, and the modeling of the bent-straight waveguide couplers.

Assuming that all transitions inside the coupler regions are sufficiently smooth, such that reflections do not play a significant role for the resonator functioning, we further restrict the model to unidirectional wave propagation, as indicated by the arrows in Figure 1. Depending on the specific configuration, this assumption can be justified or not.

Go to top

Microresonators model: Description

Consider coupler (I) first. Suppose that the straight cores support $N_{\mbox{\scriptsize s}}$ guided modes with propagation constants $\beta_{\mbox{\scriptsize s}q}$ , $q=1,\ldots,N_{\mbox{\scriptsize s}}$ . For the cavity, $N_{\mbox{\scriptsize b}}$ bend modes are taken into account. Due to the radiation losses, their propagation constants $\gamma_{\mbox{\scriptsize b}p} = \beta_{\mbox{\scriptsize b}p} - \mbox{i}\alpha_{\mbox{\scriptsize b}p}$ , $p = 1,\ldots,N_{\mbox{\scriptsize b}}$ , are complex valued [4]. Here $\beta_{\mbox{\scriptsize s}q}$ , $\beta_{\mbox{\scriptsize b}p}$ and $\alpha_{\mbox{\scriptsize b}p}$ are real positive numbers. The variables $A_{q}$ , $B_{q}$ , and $a_{p}$ , $b_{p}$ , denote the directional amplitudes of the properly normalized ``forward'' propagating (clockwise direction, cf. Figure 1) basis modes in the respective coupler port planes, combined into amplitude (column) vectors $\boldsymbol {A}$ , $\boldsymbol {B}$ , and $\boldsymbol {a}$ , $\boldsymbol {b}$ . A completely analogous reasoning applies to the second coupler, where a symbol $\tilde{~}$ identifies the mode amplitudes $\boldsymbol {\tilde{A}}$ , $\boldsymbol {\tilde{B}}$ , and $\boldsymbol {\tilde{a}}$ , $\boldsymbol {\tilde{b}}$ at the port planes.

The model of coupler for unidirectional wave propagation through the coupler regions provides scattering matrices S, $\tilde{\mbox{\sf {S}}}$ , such that the coupler operation is represented as

(1)

Outside the coupler regions the bend modes used for the description of the field in the cavity propagate independently, with the angular / arc-length dependence given by their propagation constants. Hence the amplitudes at the entry and exit ports of the connecting cavity segments are related to each other as

and

(2)

where $\tilde{\mbox{\sf {G}}}$ are $N_{\mbox{\scriptsize b}} \times N_{\mbox{\scriptsize b}}$ diagonal matrices with entries ${\sf {G}}_{p,p}=\exp{(-\mbox{i}\gamma_{\mbox{\scriptsize b}p} L)}$ and $\tilde{\sf {G}}_{p,p}=\exp{(-\mbox{i}\gamma_{\mbox{\scriptsize b}p} \tilde{L})}$ , respectively, for $p = 1,\ldots,N_{\mbox{\scriptsize b}}$ .

For the guided wave scattering problem, modal powers and are prescribed at the In-port A and at the Add-port of the resonator, and one is interested in the transmitted powers at port B and the backward dropped powers at port .
The linear system established by equations (1) and (2) is to be solved for and , given values of and .
Due to the linearity of the device the restriction to an excitation in only one port, here port A, with no incoming Add-signal , is sufficient.
In case of a configuration with single mode cavity and bus cores, one obtains the familiar explicit, parameterized expressions for the transmitted and dropped power, for the free spectral range and the resonance width, for finesse and Q-factor of the resonances, etc[3].

Go to top

Resonators spectral response

Resonances appear as a drop in the transmitted power P_T, and a simultaneous peak in the dropped power P_D.
To get a spectral response of a resonator, for a series of wavelengths solve the linear system established by equations (1) and (2) for and , given values of and .
That means, for a series of wavelengths one must first get the bent mode propagation constants γ and the coupler scattering matrices S.
For a sufficiently small wavelength interval, one can avoid the above time consuming computations by using interpolated γ and S [5].
- In order to use interpolation technique, the scattering matrix of a coupler is redefined at a point (otherwise it is defined for a certain interval in z direction).
- Using the bent mode propagation constants and the redefined coupler scattering matrices S at two reference wavelengths (linear interpolation) or at three reference wavelengths (quadratic interpolation), by interpolation one gets γ and S for series of wavelengths.
- Using these interpolated values of γ, solve equations (1) and (2) for through and drop power.

Go to top

Microresonatosr simulator: Implementation

Relevent files

mr.h, mr.c

Circular cavity microresonator (More)

Go to top

Microresonators simulator: Example

Go to top

References

K. R. Hiremath, R. Stoffer, and M. Hammer.
Modeling of circular integrated optical microresonators by 2-D frequency domain coupled mode theory.
2005 (accepted).
K. Okamoto.
Fundamentals of Optical Waveguides.
Academic Press, U.S.A, 2000.
M. Hammer, K. R. Hiremath, and R. Stoffer.
Analytical approaches to the description of optical microresonator devices.
In M. Bertolotti, A. Driessen, and F. Michelotti, editors, Microresonators as building blocks for VLSI photonics, volume 709 of AIP conference proceedings, pages 48-71. American Institute of Physics, Melville, New York, 2004.
K. R. Hiremath, M. Hammer, S. Stoffer, L. Prkna, and J. Ctyroký.
Analytic approach to dielectric optical bent slab waveguides.
Optical and Quantum Electronics, 37(1-3):37-61, January 2005.
K. R. Hiremath.
Coupled mode theory based modeling and analysis of circular optical microresonators
Ph. D. thesis, University of Twente, The Netherlands, October 2005.

Go to top