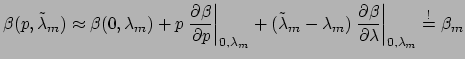Next: Existing approaches for modeling
Up: Ring-resonator theory
Previous: Finesse and quality factor
Contents
Tuning
The realization and actual performance of the resonators are constrained by
several factors, e.g. an accurate definition of the resonance wavelengths
requires a high degree control of the geometrical parameters, temperature
dependant changes in the material parameters detune the spectral
response. Active (e.g. electro-optical, thermo-optical) tuning of the
resonators greatly relaxes these constraints. This is quite essential for
stable performance of the devices. See Ref. [38] and the references
quoted there for further details. Here we outline a framework for the modeling
of tuning.
As explained in Section 1.4.3, at resonance the condition
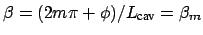 holds for the cavity
mode propagation constant, where the integer
holds for the cavity
mode propagation constant, where the integer 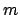 gives the order of the
resonance. Assume that the wavelength dependence of the propagation constant
gives the order of the
resonance. Assume that the wavelength dependence of the propagation constant
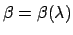 is given. Then one can write
is given. Then one can write
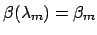 , where
, where
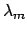 is the resonance wavelength associated with
the resonant cavity mode propagation constant
is the resonance wavelength associated with
the resonant cavity mode propagation constant 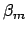 .
.
Disregarding its influence on the response of the (short) couplers as a first
approximation, a tuning mechanism is modeled by a parameter 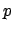 , which affects
mainly the field propagation along the cavity. Thus now, besides the
wavelength, the cavity mode propagation constant also depends on the tuning
parameter, i.e.
, which affects
mainly the field propagation along the cavity. Thus now, besides the
wavelength, the cavity mode propagation constant also depends on the tuning
parameter, i.e.
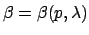 , with
, with 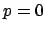 representing the
original state:
representing the
original state:
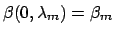 .
.
With the tuning applied, the resonance of order 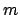 is shifted towards a new
wavelength
is shifted towards a new
wavelength
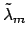 , such that
, such that
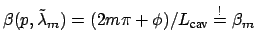 is satisfied again. A
linear approximation in the tuning parameter and in the wavelength differences
is satisfied again. A
linear approximation in the tuning parameter and in the wavelength differences
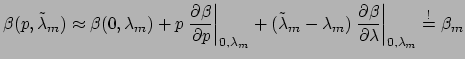 |
(1.19) |
leads to an expression for the shift in the wavelength
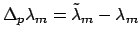 that is affected by the tuning mechanism
that is affected by the tuning mechanism
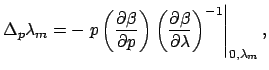 |
(1.20) |
which on simplification by using Equation (1.9) leads to
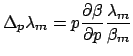 or or 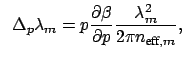 |
(1.21) |
i.e. the wavelength shift compensates the change in the cavity mode
propagation constant due to a nonzero perturbation strength 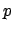 . Note that
the wavelength shift does not depend on the length of the cavity. If
available, the effective group index
. Note that
the wavelength shift does not depend on the length of the cavity. If
available, the effective group index
 according to
Equation (1.12) can replace the effective index
according to
Equation (1.12) can replace the effective index
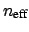 in Equation (1.21).
in Equation (1.21).
We are specifically interested in tuning effected by the change of the cavity
core permittivity (i.e. refractive index). For further details about this,
see Section 2.5 and
Section 4.6.




Next: Existing approaches for modeling
Up: Ring-resonator theory
Previous: Finesse and quality factor
Contents
Kirankumar Hiremath
2005-09-23
![]() holds for the cavity
mode propagation constant, where the integer
holds for the cavity
mode propagation constant, where the integer ![]() gives the order of the
resonance. Assume that the wavelength dependence of the propagation constant
gives the order of the
resonance. Assume that the wavelength dependence of the propagation constant
![]() is given. Then one can write
is given. Then one can write
![]() , where
, where
![]() is the resonance wavelength associated with
the resonant cavity mode propagation constant
is the resonance wavelength associated with
the resonant cavity mode propagation constant ![]() .
.
![]() , which affects
mainly the field propagation along the cavity. Thus now, besides the
wavelength, the cavity mode propagation constant also depends on the tuning
parameter, i.e.
, which affects
mainly the field propagation along the cavity. Thus now, besides the
wavelength, the cavity mode propagation constant also depends on the tuning
parameter, i.e.
![]() , with
, with ![]() representing the
original state:
representing the
original state:
![]() .
.
![]() is shifted towards a new
wavelength
is shifted towards a new
wavelength
![]() , such that
, such that
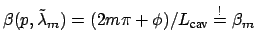 is satisfied again. A
linear approximation in the tuning parameter and in the wavelength differences
is satisfied again. A
linear approximation in the tuning parameter and in the wavelength differences