Comparison with FDTD results

As an attempt for a further validation of our results on bend modes we have considered the following numerical experiment. Embedded in a common background, the core of a straight slab waveguide is placed in the vicinity of a ring shaped core of the same width. If a guided wave is launched into the straight channel, by evanescent coupling it excites optical waves that travel around the ring. If, for given polarization, the bent ring waveguide supports only a single low-loss bend mode, one can expect that a field with the corresponding profile establishes itself after a suitable propagation distance. The experiment is carried out in the time domain, with a ramped-up, subsequently time-harmonic excitation, that is advanced over a limited time interval, such that resonance effects can be excluded. Allowing the ``wave front'' to propagate once around the ring, a radial field cross section e.g. at an angular position of $90^\circ$ after the in-coupling region can be expected to give an approximation to the bend mode profile. By observing the exponential decay of the ``stationary'' field for an angular segment after that region, one can estimate the attenuation of the bend mode.

We have applied a standard Finite Difference Time Domain (FDTD) scheme [94,95], where a computational window of $80 \times 58\,\mu$m$^2$ is discretized uniformly by a mesh with step sizes of $0.05\,\mu$m. Perfectly matched layer (PML) boundary conditions enclose the computational domain, with a width of $8$ points, a quadratic envelope, and a strength such that the theoretical reflectivity of a wave propagating through the background material at normal incidence is $10^{-6}$. The interior of the computational window contains the ring with parameters as given for Figure 2.6 and the straight waveguide with the same refractive index profile, with a gap of $0.5\,\mu$m in between. A modal field is launched into the straight core using the total field /scattered field approach [55]. Its amplitude is raised according to a half-Gaussian curve with a waist of $5\,$fs, with the maximum being reached at $40\,$fs. After this time, the incident field amplitude is kept constant. The simulation runs for a time of $1.1\,$ps with a time step of $0.1\,$fs, after which the ramp of the wave has gone around the ring approximately once.

Figure: Bend mode profiles as determined by a FDTD simulation (continuous line) and by the analytical model (dashed curve), for a configuration with $(n_{\mbox{\scriptsize s}}, n_{\mbox{\scriptsize f}}, n_{\mbox{\scriptsize c}})=(1.6, 1.7, 1.6)$, $d=1\,\mu$m, $R=25\,\mu$m, $\lambda=1.3\,\mu$m. Here the mode profiles are normalized to a unit maximum.

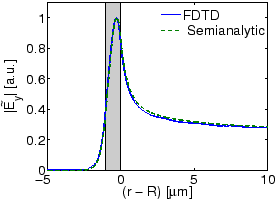Figure 2.6 shows an excellent agreement of the approximation for the bend mode profile obtained in this way with the result of the analytical bend mode solver. We also found a very good agreement of the attenuation constant $\alpha = 0.01949\,\mu$m$^{-1}$ estimated by the FDTD simulation with the analytic result $\alpha = 0.01978\,\mu$m$^{-1}$. Hence comparisons of this kind can confirm the expectation that the bend modes as introduced in Eq. (2.1) are indeed suitable basis fields for a (2-D) description of cylindrical microresonator configurations.