Higher order bend modes

For cylindrical cavities with relatively high radial refractive index contrast, also higher order bend modes can be relevant for an adequate representation of resonant field patterns [96,97,98]. Table 2.3 summarizes results for propagation constants of fundamental and first order modes of both polarizations for a nonsymmetric slab with decreasing bend radius. In a straight configuration, the refractive index profile supports two guided modes per polarization orientation.

Table: Propagation constants $\gamma = \beta -$   i$\,\alpha$ of fundamental and first order modes for bends with $(n_{\mbox{\scriptsize s}}, n_{\mbox{\scriptsize f}}, n_{\mbox{\scriptsize c}}) = (1.6, 1.7, 1.55)$, $d=2\,\mu$m, $\lambda = 1.55\,\mu$m, for different bend radii $R$. The value $R=\infty$ indicates the corresponding (bimodal) straight waveguide.

	TE$_{0}$		TE$_{1}$
$R\ [\,\mu$m$]$	$\beta /k$	$\alpha / k$	$\beta /k$	$\alpha / k$
$\infty$	$1.6775$	$-$	$1.6164$	$-$
$150$	$1.6663$	$\approx 0$	$1.6037$	$1.2117\cdot 10^{-7}$
$100$	$1.6611$	$1.0984\cdot 10^{-12}$	$1.5979$	$1.7606\cdot 10^{-5}$
$50$	$1.6473$	$9.6704\cdot 10^{-7}$	$1.5818$	$1.5113\cdot 10^{-3}$
$20$	$1.6185$	$1.8299\cdot 10^{-3}$	$1.5283$	$1.4205\cdot 10^{-2}$
$10$	$1.5890$	$1.6025\cdot 10^{-2}$	$1.4381$	$3.4287\cdot 10^{-2}$

	TM$_{0}$		TM$_{1}$
$R\ [\,\mu$m$]$	$\beta /k$	$\alpha / k$	$\beta /k$	$\alpha / k$
$\infty$	$1.6758$	$-$	$1.6134$	$-$
$150$	$1.6645$	$\approx 0$	$1.6004$	$3.5259\cdot 10^{-7}$
$100$	$1.6593$	$1.8446\cdot 10^{-12}$	$1.5946$	$3.4692\cdot 10^{-5}$
$50$	$1.6451$	$1.2668\cdot 10^{-6}$	$1.5791$	$2.0368\cdot 10^{-3}$
$20$	$1.6156$	$2.1391\cdot 10^{-3}$	$1.5273$	$1.7868\cdot 10^{-2}$
$10$	$1.5855$	$1.8702\cdot 10^{-2}$	$1.4391$	$4.6089\cdot 10^{-2}$

Just as for the fundamental fields, the attenuation of the first order modes grows with decreasing bend radius. Figure 2.7 shows that the significantly higher loss levels of the first order modes are accompanied by larger field amplitudes in the exterior region and by a wider radial extent of the mode profiles.

Figure: Fundamental and first order TE modes for the bends of Table 2.3, absolute values of the basic profile component $\tilde{E}_y$ of structures with radii $R = 100$, $50$, and $20\,\mu$m.

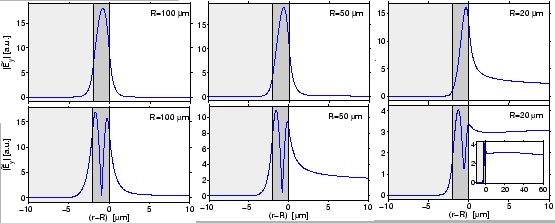Figure 2.8 illustrates the spatial evolution of the TE$_{0}$ and TE$_{1}$ modes for a small configuration with $R=20\,\mu$m. Major differences between the plots for the single fundamental and first order fields are the faster decay of the TE$_{1}$ mode and the minimum in the radial distribution of that field.

Figure: Spatial evolution and interference of the fundamental and first order TE modes, for a configuration of Table 2.3 with $R=20\,\mu$m. The propagation of the TE$_{0}$ mode (left), of the TE$_{1}$ mode (center), and of a superposition of these (right) is evaluated. The plots show the absolute value $\vert E_y\vert$ (top) and snapshots of the time harmonic physical field $E_y$ (bottom).

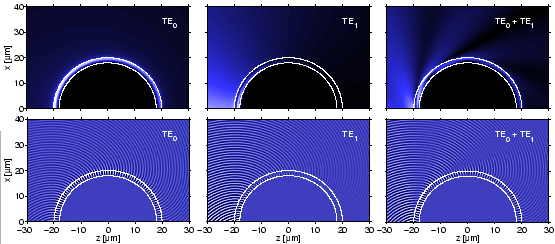The last column of Figure 2.8 gives an example for an interference pattern that is generated by a superposition of both modes. Normalized profiles with unit amplitudes and real, positive $\tilde{E}_y(R)$ are initialized at $\theta=0$, or $z=0$, respectively (cf. Figure 2.1). In the core region one observes the familiar beating process, here in the angular direction, with intensity maxima shifting periodically between the center and the outer rim of the ring. In the exterior region, the mode interference results in a ray-like pattern, where rapidly diverging bundles of waves propagate in directions tangential to the ring, originating from regions around the intensity maxima at the outer ring interface. These phenomena are obscured by the fast decay of the first order mode.

Apart from the fundamental and first order fields, further higher order modes can be found for the bent slabs of Table 2.3. While the TE$_{0}$ and TE$_{1}$ modes considered so far can be viewed as being related to the guided modes supported by a straight slab with the same refractive index profile and thickness, the profiles shown in Figure 2.9 are not related to guided modes of that straight waveguide.

For these modes, the classification by the number of minima in the absolute value of the mode profile can still be applied; also the systematics of larger attenuation and higher exterior field levels for growing mode order remains valid.

Figure: Higher order TE modes for a bend as considered for Table 2.3 with $R = 100\,\mu$m. The corresponding propagation constants $\gamma /k$ are $1.5347 -$   i$\, 2.8974 \cdot 10^{-3}$ (TE$_{2}$), $1.5094 -$   i$\, 5.7969 \cdot 10^{-3}$ (TE$_{3}$), and $1.4891 -$   i$\, 6.1955 \cdot 10^{-3}$ (TE$_{4}$), respectively. The insets clearly show the decay of the mode profiles for $r \rightarrow \infty$ after an initial growth of the field in the cover region.

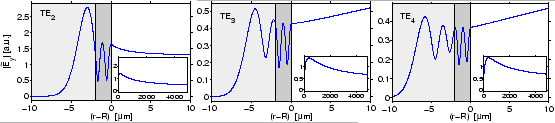In contrast to the two lowest order fields, these higher order modes exhibit pronounced intensity maxima in the interior region. Apparently, for the present nonsymmetric bend, this indicates the transition to the regime of whispering gallery modes, which is discussed below.