Tuning

From a practical point of view, the ability to tune the spectral response of the resonators is an essential feature. As mentioned in Section 1.4.5, a tuning mechanism can relax otherwise quite demanding fabrication tolerances, and it can also help to eliminate any unwanted temperature induced deviations of the spectral response.

For the applications of microresonators as tunable wavelength filters, suitable materials are introduced that permit to change slightly the refractive index of the cavity core by external mechanisms like electro- or thermo-optic effects. Then using Eq. (1.21), shifts in resonance wavelengths due to changes of the core refractive index are given by

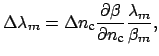$$\Delta \lambda_{m} = \Delta n_{\mbox{\scriptsize c}} \frac{\partial \beta}{\partial n_{\mbox{\scriptsize c}}} \frac{\lambda_{m}}{\beta_{m}},$$ (4.15)

where the derivative of the phase propagation constant with respect to the core refractive index can be approximated by Eq. (2.31) as

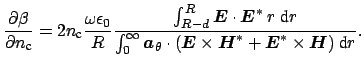$$\frac{\partial \beta}{\partial n_{\mbox{\scriptsize c}}} = 2 n_{\... ...boldsymbol {H}^{*} + \boldsymbol {E}^{*} \times \boldsymbol {H} ) \ \mbox{d}r}.$$ (4.16)

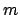Here $\boldsymbol {E}, \boldsymbol {H}$ are the electric field and magnetic field of the cavity mode associated with the $m$'th order resonance.