To proceed further, the CMT equations are solved by numerical means. Brief
details about the procedures are given in Section 3.4; the result
can be stated in terms of a transfer matrix
T that relates the CMT
amplitudes at the output plane
![]() to the amplitudes at the
input plane
to the amplitudes at the
input plane
![]() of the coupler region:
of the coupler region:
Outside the coupler (i.e. outside the region
![]() ), it is assumed that the interaction
between the fields associated with the different cores is negligible. The
individual modes propagate undisturbed according to the harmonic dependences
on the respective propagation coordinates, such that the external fields are:
), it is assumed that the interaction
between the fields associated with the different cores is negligible. The
individual modes propagate undisturbed according to the harmonic dependences
on the respective propagation coordinates, such that the external fields are:
For a typical coupler configuration, the guided modal fields of the straight
waveguide are well confined to the straight core. On the contrary,
due to the radiative nature of the fields, the bend mode profiles can extend
far beyond the outer interface of the bent waveguide.
Depending upon the specific physical configuration, the extent of these
radiative parts of the fields varies, such that also outside the actual
coupler region, the field strength of the bend modes in the region close
to the straight core may be significant. Therefore, to assign
the external mode amplitudes ![]() ,
, ![]() , it turns out to be necessary
to project the coupled field on the straight waveguide modes.
, it turns out to be necessary
to project the coupled field on the straight waveguide modes.
At a sufficient distance from the cavity, in the region where
only the straight waveguide is present, the total field
![]() can be expanded into the complete set of modal
solutions of the eigenvalue problem for the straight waveguide. The basis
set consists of a finite number of guided modes
can be expanded into the complete set of modal
solutions of the eigenvalue problem for the straight waveguide. The basis
set consists of a finite number of guided modes
![]() and a nonguided,
radiative part
and a nonguided,
radiative part
![]() , such that
, such that
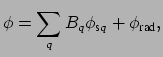 |
(3.18) |
Thus, given the solution (3.15) of the coupled mode equations in the form of
the transfer matrix
T, the scattering matrix
S that relates
the amplitudes ![]() ,
, ![]() ,
, ![]() ,
, ![]() of the external fields as required
in equation (1.1) is defined as
of the external fields as required
in equation (1.1) is defined as
A lower left block is filled with entries
![]() and
and
![]() ,
for
,
for
![]() and
and
![]() ,
respectively, that incorporate the projections.
All other coefficients of
P and
Q are zero.
,
respectively, that incorporate the projections.
All other coefficients of
P and
Q are zero.